Definition

The concept HDVF describes the requirements for Homological Discrete Vector Fields (HDVF for short) , a theory of computational homology unifying discrete Morse theory and effective homology. HDVFs were introduced by Aldo Gonzalez-Lorenzo in his PhD (see [AGL,2017], [AGL,2016]).

A HDVF is a combinatorial tool computing the homology of a chain complex (described by the AbstractChainComplex concept) including "geometric" information such as homology and cohomology generators.

As described in the user manual description, an HDVF is:

a partition of the cells of the underlying complex into three classes: primary (P), secondary (S) and critical (C), together with partial invertibility conditions for the boundary operator,
an associated reduction \((f,g,h)\) from the chain complex onto a chain complex generated by critical cells and a reduced boundary. A HDVF is perfect when the reduced boundary is null; in this case, the maps \(f\) and \(g\) (and their duals) provide homology and cohomology information (generators, annotation...).

More precisely, a HDVF over a chain complex C, derived from a complex K, is a partition of the cells: \(K = P\coprod S\coprod C\) with \(P\) primary cells, \(S\) secondary cells and \(C\) critical cells, such that the sub-matrix:

\[\partial (S)|_P\text{ is invertible.} \]

In what follows, given \(q\in \mathbb N\) and \(G\) a sub-group of the qth chain group \(C_q\), we denote by:

\(i_G\) the inclusion \(G\to C_q\)
\(j_G\) the projection \(C_q\to G\)

That is, for all \(q\in \mathbb N\), if

\[\mathrm{Mat}(\partial_q) = \begin{array}{lc} & P_q \ \ \ \ S_q \ \ \ \ C_q \\ \begin{array}{l} P_{q-1} \\ S_{q-1} \\ C_{q-1} \\ \end{array} & \left(\begin{array}{ccc} \star & D_{PS} & \star \\ \star & \star & \star \\ \star & \star & \star \\ \end{array}\right)\\ \end{array} \]

then \(D_{PS}\), the matrix of \(j_P\circ \partial\circ i_S\), also written \(\partial (S)|_P\) is invertible.

In order to build a perfect HDVF, a pairing operation called A() associates (under conditions) two critical cells (becoming PRIMARY and SECONDARY) and updates the reduction in time \(\mathscr O(n^2)\). Intuitively, this operation bears some similitudes (see users guide) with discrete Morse theory's DGVF arrows (and an HDVF can always be represented by such a vector field - possibly with cycles). Given a HDVF \(X = (P,S,C)\), A operation between two cells \((\gamma_1, \gamma_2)\) of respective dimension \(q/q+1\) is valid if \((P',S',C') = (P\cup\{\gamma_1\}, P\cup\{\gamma_2\}, C\backslash\{\gamma_1,\gamma_2\})\) is a HDVF (ie. if \(j_{P'}\circ \partial\circ i_{S'}\) is still invertible). This is actually the case if and only if \(\langle d(\gamma_2), \gamma_1 \rangle\) (with \(d\) the reduced boundary operator) is invertible. This condition is called the validity condition for A; all the find_pair_A() and find_pairs_A() methods search for such valid pairs.

Starting from this operation, HDVF provides two methods to generate perfect HDVFs (and hence compute homology):

compute_perfect_hdvf() which computes a perfect HDVF by chosing at each step the first A-pairings available (depending on cells ordering in the chain complex)
compute_rand_perfect_hdvf() which computes a perfect random HDVF by chosing at each step a rand A-pairing among all possible ones (this option is thus slower)

For efficiency, the HDVF reduction can be computed partially:

compute only the reduced boundary (option OPT_BND): to get Betti numbers
compute \(\partial'\) together with \(h\) and \(g\) (option OPT_G): to get homology generators
compute \(\partial'\) together with \(h\) and \(f\) (option OPT_F): to get co-homology generators
compute the full reduction (option OPT_FULL): to get the full homological / cohomological information

Let us consider a simple cubical complex example (see Cubical chain complexes for an introduction). In what follows, PRIMARY cells are coloured green, SECONDARY are coloured red and critical blue. The picture below shows an initial empty HDVF where all cells are critical:

The boundary matrix of \(\partial_2\) (which equals the reduced boundary matrix as the HDVF is empty) for \(\mathbb Z\)-homology is (cells are identified by their Khalimsky coordinates):

\[\mathrm{Mat}(\partial_2) = \begin{array}{lc} & (3,1)\\ \begin{array}{l} (3,0) \\ (2,1) \\ (4,1) \\ (3,2) \\ \end{array} & \left(\begin{array}{c} 1 \\ -1 \\ 1 \\ -1 \\ \end{array}\right)\\ \end{array} \]

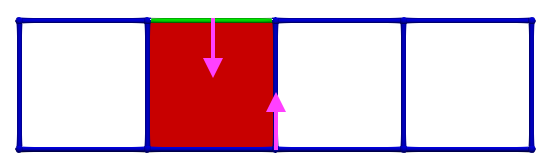
Let us consider \(\gamma_2 = (3,1)\) and \(\gamma_1 = (3,2)\), the condition for A is valid (-1 is invertible). The following images illustrates this pairing in discrete Morse theory "style" (pink arrow in left complex) and the resulting HDVF (right complex).

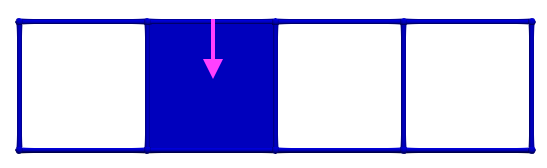
The reduced boundary matrix in dimension 2 becomes empty and the matrix of \(d_1\) is similar to the boundary matrix \(\partial_1\) with the row/colums associated to previous cells removed.

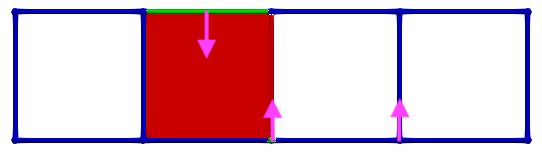
Thus, if we now consider \(\gamma_2 = (4,1)\) and \(\gamma_1 = (4,0)\), the condition for A is valid; cells can be paired and we obtain the following HDVF:

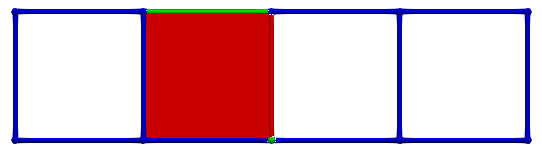
The process can be continued step by step:

Until we eventually get a perfect HDVF:

Each hole is identified by a critical cell and the \(g\) map of the reduction provides associated homology generators (highlighted in blue):

A corresponding cohomology generators (highlighted in pink):

Has models
: CGAL::Homological_discrete_vector_field::Hdvf_core<IntegralDomainWithoutDivision, AbstractChainComplex, SparseChain, Sparse_matrix>
: CGAL::Homological_discrete_vector_field::Hdvf<IntegralDomainWithoutDivision, AbstractChainComplex>
: CGAL::Homological_discrete_vector_field::Hdvf_persistence<IntegralDomainWithoutDivision, AbstractChainComplex>
: CGAL::Homological_discrete_vector_field::Hdvf_duality<IntegralDomainWithoutDivision, AbstractChainComplex>

See also: AbstractChainComplex; IntegralDomainWithoutDivision; SparseChain; SparseMatrix

How to describe constants declared in the namespace Homological_discrete_vector_field and used everywhere? PSC_flag, options, exporttype*

[AGL, 2017] Aldo Gonzalez-Lorenzo, Alexandra Bac, Jean-Luc Mari, Pedro Real. Allowing cycles in discrete Morse theory, Topology and its Applications, Volume 228, 2017, Pages 1-35.

[AGL, 2016] Aldo Gonzalez-Lorenzo. Computational Homology Applied to Discrete Objects. Discrete Mathematics [cs.DM]. Aix-Marseille Université; Universidad de Sevilla, 2016.

Examples: HDVF/hdvf_cubical.cpp, HDVF/hdvf_simplicial.cpp, HDVF/hdvf_surface_mesh_simplicial.cpp, HDVF/main_dual_hdvf.cpp, HDVF/main_hdvf.cpp, and HDVF/main_per_hdvf.cpp.

Concepts
concept	Cell_pair
	Structure to represent data for HDVF operations (pairs of cells). More...

Types
typedef unspecified_type	Complex
	Type of underlying chain complex (a model of `AbstractChainComplex`).

typedef Complex::Coefficient_ring	Coefficient_ring
	Type of coefficients used to compute homology.

typedef unspecified_type	Sparse_chain
	Type of sparse chains (a model of `SparseChain`).

typedef unspecified_type	Sparse_matrix
	Type of sparse matrices (a model of `SparseMatrix`).

typedef Sparse_chain< CoefficientType, CGAL::OSM::COLUMN >	Column_chain
	Type of column-major chains.

typedef Sparse_chain< CoefficientType, CGAL::OSM::ROW >	Row_chain
	Type of row-major chains.

typedef Sparse_matrix< CoefficientType, CGAL::OSM::COLUMN >	Column_matrix
	Type of column-major sparse matrices.

typedef Sparse_matrix< CoefficientType, CGAL::OSM::ROW >	Row_matrix
	Type of row-major sparse matrices.

Functions to find valid pairs for <tt>A()</tt> operations
virtual Cell_pair	find_pair_A (int q, bool &found) const
	Finds a valid Cell_pair of dimension q / q+1 for A.

virtual Cell_pair	find_pair_A (int q, bool &found, size_t gamma) const
	Finds a valid Cell_pair for A containing `gamma` (a cell of dimension `q`)

virtual std::vector< Cell_pair >	find_pairs_A (int q, bool &found) const
	Finds all valid Cell_pair of dimension q / q+1 for A.

virtual std::vector< Cell_pair >	find_pairs_A (int q, bool &found, size_t gamma) const
	Finds all valid Cell_pair for A containing `gamma` (a cell of dimension `q`)

HDVF functions and operations
void	A (size_t gamma1, size_t gamma2, int q)
	A operation: pairs two critical cells.

std::vector< Cell_pair >	compute_perfect_hdvf (bool verbose=false)
	Computes a perfect HDVF.

std::vector< Cell_pair >	compute_rand_perfect_hdvf (bool verbose=false)
	Computes a random perfect HDVF.

Getters
std::vector< std::vector< size_t > >	flag (PSC_flag flag) const
	Gets cells with a given `PSC_flag` in any dimension.

std::vector< size_t >	psc_flags (PSC_flag flag, int q) const
	Gets cells with a given `PSC_flag` in dimension `q`.

PSC_flag	psc_flag (int q, size_t tau) const
	Gets the `PSC_flag` of the cell `tau` in dimension `q`.

int	hdvf_opts ()
	Gets HDVF option.

const Row_matrix &	matrix_f (int q) const
	Gets the row-major matrix of \(f\) (from the reduction associated to the HDVF).

const Column_matrix &	matrix_g (int q) const
	Gets the column-major matrix of \(g\) (from the reduction associated to the HDVF).

const Column_matrix &	matrix_h (int q) const
	Gets the column-major matrix of \(h\) (from the reduction associated to the HDVF).

const Column_matrix &	matrix_dd (int q) const
	Gets the column-major matrix of \(\partial'\), reduced boundary operator (from the reduction associated to the HDVF).

bool	is_perfect_hdvf ()
	Tests if a HDVF is perfect.

Output functions
std::ostream &	write_matrices (std::ostream &out=std::cout) const
	Writes the matrices of the reduction.

std::ostream &	write_reduction (std::ostream &out=std::cout) const
	Writes the homology and cohomology reduction information.

std::ostream &	write_hdvf_reduction (std::ostream &out)
	Writes a HDVF and its reduction to a stream.

std::istream &	read_hdvf_reduction (std::istream &in)
	Reads a HDVF and its reduction from a stream.

virtual std::vector< std::vector< int > >	psc_labels () const
	Exports primary/secondary/critical labels (in particular for vtk export).

virtual Column_chain	homology_chain (size_t cell_index, int q) const
	Returns a chain containing the homology generator associated to `cell_index` (critical cell) of dimension `q` (in particular for vtk export).

virtual Column_chain	cohomology_chain (size_t cell_index, int dim, bool co_faces=false) const
	Returns a chain containing the cohomology generators associated to `cell_index` (critical cell) of dimension `q` (in particular for vtk export).

Member Function Documentation

◆ A()

void HDVF::A	(	size_t	gamma1,
		size_t	gamma2,
		int	q
	)

A operation: pairs two critical cells.

A pair of critical cells \((\gamma_1, \gamma_2)\) of respective dimension q and q+1 is valid for A if \(\langle \partial_{q+1}(\gamma_2), \gamma_1 \rangle\) is invertible. After the A() operation, \(\gamma_1\) becomes PRIMARY, \(\gamma_2\) becomes SECONDARY. The A functions updates the reduction accordingly (in time \(\mathscr O(n^2)\)).

◆ cohomology_chain()

virtual Column_chain HDVF::cohomology_chain	(	size_t	cell_index,
		int	dim,
		bool	co_faces = `false`
	)		const

virtual

Returns a chain containing the cohomology generators associated to cell_index (critical cell) of dimension q (in particular for vtk export).

The method exports:

the chain \(f^\star(\sigma)\) for \(\sigma\) the cell of index cell_index and dimension q,
or the co-faces of this chain if co_faces is true (sometimes easier to view cohomology generators)

Below, a sample mesh with, (left) homology generators, (right) two examples of cohomology generators (corresponding generators/co-generators bear similar colours):

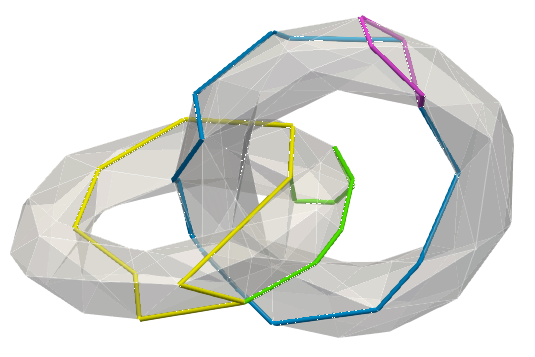
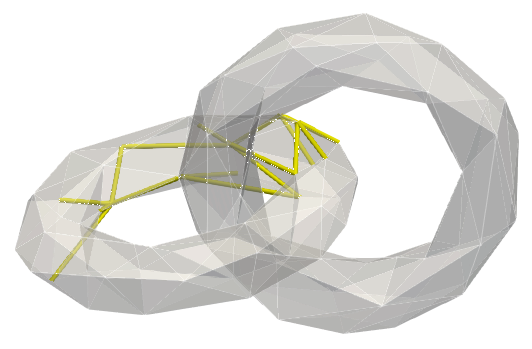
The same generators displayed through their co-faces:

All homology / cohomology generators:

Returns: A column-major chain.

◆ compute_perfect_hdvf()

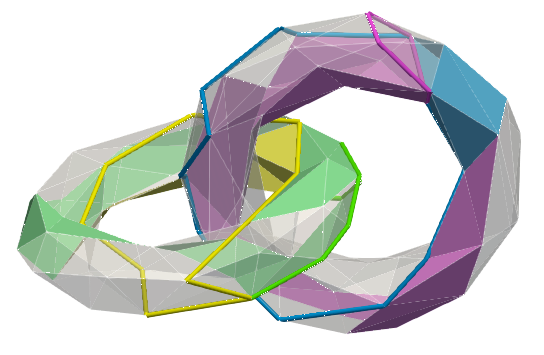
std::vector< Cell_pair > HDVF::compute_perfect_hdvf ( bool verbose = false )

Computes a perfect HDVF.

As long as valid pairs for A exist, the function selects the first available pair (returned by find_pair_A()) and applies the corresponding A() operation. If the IntegralDomainWithoutDivision of coefficients is a field, this operation always produces a perfect HDVF (ie. the reduced boundary is null and the reduction provides homology and cohomology information).

If the HDVF is initially not trivial (some cells have already been paired), the function completes it into a perfect HDVF.

Parameters

verbose If true, all intermediate reductions are printed out.

◆ compute_rand_perfect_hdvf()

std::vector< Cell_pair > HDVF::compute_rand_perfect_hdvf ( bool verbose = false )

Computes a random perfect HDVF.

As long as valid pairs for A exist, the function selects a random pair (among pairs returned by find_pairs_A()) and applies the corresponding A() operation. If the IntegralDomainWithoutDivision of coefficients is a field, this operation always produces a perfect HDVF (ie. the reduced boundary is null and the reduction provides homology and cohomology information).

If the HDVF is initially not trivial (some cells have already been paired), the function randomly completes it into a perfect HDVF.

Parameters

verbose If true, all intermediate reductions are printed out.

◆ find_pair_A() [1/2]

virtual Cell_pair HDVF::find_pair_A	(	int	q,
		bool &	found
	)		const

virtual

Finds a valid Cell_pair of dimension q / q+1 for A.

The function searches a pair of critical cells \((\gamma_1, \gamma2)\) of dimension q / q+1, valid for A (ie. such that \(\langle \partial_{q+1}(\gamma_2), \gamma_1 \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

q	Lower dimension of the pair.
found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pair_A() [2/2]

virtual Cell_pair HDVF::find_pair_A	(	int	q,
		bool &	found,
		size_t	gamma
	)		const

virtual

Finds a valid Cell_pair for A containing gamma (a cell of dimension q)

The function searches a cell \(\gamma'\) such that one of the following conditions holds:

\(\gamma'\) has dimension q+1 and \((\gamma, \gamma')\) is valid for A (ie. such that \(\langle \partial_{q+1}(\gamma'), \gamma \rangle\) invertible),
\(\gamma'\) has dimension q-1 and \((\gamma', \gamma)\) is valid for A (ie. such that \(\langle \partial_{q}(\gamma), \gamma' \rangle\) invertible).

Parameters

q	Dimension of the cell `gamma`.
found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
gamma	Index of a cell to pair.

◆ find_pairs_A() [1/2]

virtual std::vector< Cell_pair > HDVF::find_pairs_A	(	int	q,
		bool &	found
	)		const

virtual

Finds all valid Cell_pair of dimension q / q+1 for A.

The function searches all pairs of critical cells \((\gamma_1, \gamma2)\) of dimension q / q+1, valid for A (ie. such that \(\langle \partial_{q+1}(\gamma_2), \gamma_1 \rangle\) invertible). It returns a vector of such pairs.

Parameters

q	Lower dimension of the pair.
found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pairs_A() [2/2]

virtual std::vector< Cell_pair > HDVF::find_pairs_A	(	int	q,
		bool &	found,
		size_t	gamma
	)		const

virtual

Finds all valid Cell_pair for A containing gamma (a cell of dimension q)

The function searches all critical cells \(\gamma'\) such that one of the following conditions holds:

\(\gamma'\) has dimension q+1 and \((\gamma, \gamma')\) is valid for A (ie. such that \(\langle \partial_{q+1}(\gamma'), \gamma \rangle\) invertible),
\(\gamma'\) has dimension q-1 and \((\gamma', \gamma)\) is valid for A (ie. such that \(\langle \partial_{q}(\gamma), \gamma' \rangle\) invertible). It returns a vector of such pairs.

Parameters

q	Dimension of the cell `gamma`.
found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
gamma	Index of a cell to pair.

◆ flag()

std::vector< std::vector< size_t > > HDVF::flag ( PSC_flag flag ) const

Gets cells with a given PSC_flag in any dimension.

The function returns in each dimension the vector of cells with a given PSC_flag.

◆ homology_chain()

virtual Column_chain HDVF::homology_chain	(	size_t	cell_index,
		int	q
	)		const

virtual

Returns a chain containing the homology generator associated to cell_index (critical cell) of dimension q (in particular for vtk export).

The method exports the chain \(g(\sigma)\) for \(\sigma\) the cell of index cell_index and dimension q.

Returns: A column-major chain.

◆ is_perfect_hdvf()

bool HDVF::is_perfect_hdvf ( )

Tests if a HDVF is perfect.

The function returns true if the reduced boundary matrix is null and false otherwise.

◆ psc_flags()

std::vector< size_t > HDVF::psc_flags	(	PSC_flag	flag,
		int	q
	)		const

Gets cells with a given PSC_flag in dimension q.

The function returns the vector of cells of dimension q with a given PSC_flag.

◆ psc_labels()

virtual std::vector< std::vector< int > > HDVF::psc_labels ( ) const

virtual

Exports primary/secondary/critical labels (in particular for vtk export).

The method exports the labels of every cell in each dimension.

Returns: A vector containing, for each dimension, the vector of labels by cell index.

◆ read_hdvf_reduction()

std::istream & HDVF::read_hdvf_reduction ( std::istream & in )

Reads a HDVF and its reduction from a stream.

Reads a HDVF and its reduction from the stream in in .hdvf file format, a simple text file format (see for a specification).

◆ write_hdvf_reduction()

std::ostream & HDVF::write_hdvf_reduction ( std::ostream & out )

Writes a HDVF and its reduction to a stream.

Write a HDVF together with the associated reduction (f, g, h, d matrices) to the stream out in .hdvf file format.

◆ write_matrices()

std::ostream & HDVF::write_matrices ( std::ostream & out = std::cout ) const

Writes the matrices of the reduction.

Writes the matrices of the reduction (that is \(f\), \(g\), \(h\), \(\partial'\) the reduced boundary).

By default, writes the complex to std::cout.

◆ write_reduction()

std::ostream & HDVF::write_reduction ( std::ostream & out = std::cout ) const

Writes the homology and cohomology reduction information.

Writes the homology and cohomology reduction information (that is \(f^*\), \(g\) \(\partial'\) the reduced boundary over each critical cell).

By default, writes the complex to std::cout.

Definition

Concepts

Types

Functions to find valid pairs for <tt>A()</tt> operations

HDVF functions and operations

Getters

Output functions

Member Function Documentation

◆ A()

◆ cohomology_chain()

◆ compute_perfect_hdvf()

◆ compute_rand_perfect_hdvf()

◆ find_pair_A() [1/2]

◆ find_pair_A() [2/2]

◆ find_pairs_A() [1/2]

◆ find_pairs_A() [2/2]

◆ flag()

◆ homology_chain()

◆ is_perfect_hdvf()

◆ psc_flags()

◆ psc_labels()

◆ read_hdvf_reduction()

◆ write_hdvf_reduction()

◆ write_matrices()

◆ write_reduction()