- Authors
- Sébastien Loriot, Jane Tournois, Mael Rouxel-Labbé, Konstantinos Katrioplas, Ivan Pađen, Hossam Saeed, Ilker O. Yaz, and Sébastien Valette
Introduction
The number of elements as well as their quality are key factors for the efficiency of algorithms involving polygonal meshes: too many elements lead to high computational costs, while poorly-shaped elements may lead to numerical instabilities and inaccurate results. Remeshing techniques aim at improving the quality of a mesh by modifying its combinatorial structure and geometric embedding.
This package provides a collection of methods and classes to perform meshing and remeshing of polygonal meshes. One can distinguish between local remeshing algorithms, which work on the input using only local modifications (edge splits, collapses, flips, vertex relocations), from global remeshing algorithms, which construct a new mesh from scratch.
Another important distinction exists between combinatorial remeshing algorithms, which only modify the combinatorial structure of the mesh (i.e., its connectivity), and geometric remeshing algorithms, which also modify the position of the mesh vertices.
Selecting the most suitable remeshing algorithm depends on the specific requirements of the application.
For reference, two other CGAL packages provide related functionalities:
Outline
This manual is organized as follows:
Combinatorial Remeshing
Many algorithms require input meshes in which all faces have the same degree, or are exclusively triangles. Triangulating all polygonal faces of a mesh is therefore often necessary.
This package provides the function CGAL::Polygon_mesh_processing::triangulate_faces(), which triangulates all faces of the input polygon mesh. For each face, an approximated support plane is selected, orthogonal to the normal vector computed by CGAL::Polygon_mesh_processing::compute_face_normal(). The triangulation is performed by constructing a CGAL::Constrained_Delaunay_triangulation_2 in this plane. This approach is chosen because the constrained Delaunay triangulation maximizes the minimum angle among all triangles, given the edges of the face.
Example: PMP_Remeshing/triangulate_faces_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/triangulate_faces.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <CGAL/boost/graph/helpers.h>
#include <iostream>
#include <string>
namespace PMP = CGAL::Polygon_mesh_processing;
int main(int argc, char* argv[])
{
const char* outfilename = (argc > 2) ? argv[2] : "P_tri.off";
Mesh mesh;
if(!PMP::IO::read_polygon_mesh(filename, mesh))
{
std::cerr << "Error: Invalid input." << std::endl;
return EXIT_FAILURE;
}
{
std::cerr << "Warning: empty file?" << std::endl;
return EXIT_SUCCESS;
}
std::cout << "Input mesh is not triangulated." << std::endl;
else
std::cout << "Input mesh is triangulated." << std::endl;
for(boost::graph_traits<Mesh>::face_descriptor f : faces(mesh))
{
std::cerr << "Error: non-triangular face left in mesh." << std::endl;
}
return EXIT_SUCCESS;
}
bool triangulate_faces(const FaceRange &face_range, PolygonMesh &pmesh, const NamedParameters &np=parameters::default_values())
triangulates given faces of a polygon mesh.
Definition: triangulate_faces.h:381
bool is_triangle_mesh(const FaceGraph &g)
bool is_triangle(typename boost::graph_traits< FaceGraph >::halfedge_descriptor hd, const FaceGraph &g)
bool is_empty(const FaceGraph &g)
bool write_polygon_mesh(const std::string &fname, Graph &g, const NamedParameters &np=parameters::default_values())
std::string data_file_path(const std::string &filename)
An optional parameter, visitor, enables tracking of how faces are subdivided during triangulation. The following example demonstrates its usage.
Example: PMP_Remeshing/triangulate_faces_split_visitor_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/triangulate_faces.h>
#include <CGAL/boost/graph/copy_face_graph.h>
#include <iostream>
#include <fstream>
#include <string>
#include <unordered_map>
#include <utility>
typedef boost::graph_traits<Mesh>::face_descriptor face_descriptor;
class Insert_iterator
{
typedef std::unordered_map<face_descriptor,face_descriptor>
Container;
public:
: container(c) {}
Insert_iterator&
operator=(const std::pair<face_descriptor, face_descriptor>& p)
{
container[p.second] = p.first;
return *this;
}
operator++(int) { return *this; }
};
struct Visitor
{
typedef std::unordered_map<face_descriptor,face_descriptor>
Container;
face_descriptor qfd;
: container(container)
{}
void before_subface_creations(face_descriptor fd)
{
std::cout << "split : " << fd << " into:" << std::endl;
Container::iterator it = container.find(fd);
qfd = it->second;
container.erase(it);
}
void after_subface_created(face_descriptor fd)
{
std::cout << " " << fd;
container[fd]=qfd;
}
void after_subface_creations()
{
std::cout << std::endl;
}
};
int main(int argc, char* argv[])
{
std::ifstream input(filename);
Mesh mesh;
if (!input || !(input >> mesh) || mesh.is_empty())
{
std::cerr << "Not a valid off file." << std::endl;
return 1;
}
std::unordered_map<face_descriptor,face_descriptor> t2q;
Mesh copy;
Visitor v(t2q);
for(std::unordered_map<face_descriptor,face_descriptor>::iterator it = t2q.begin(); it != t2q.end(); ++it){
std::cout << it->first << " " << it->second << std::endl;
}
return 0;
}
Insert_iterator(Container &c)
Vector_2< Kernel > operator*(const Vector_2< Kernel > &v, const Kernel::RT &s)
void copy_face_graph(const SourceMesh &sm, TargetMesh &tm, const NamedParameters1 &np1=parameters::default_values(), const NamedParameters2 &np2=parameters::default_values())
Default new face visitor model of PMPTriangulateFaceVisitor.
Definition: triangulate_faces.h:47
Local Remeshing
Isotropic Incremental Remeshing
The incremental triangle-based isotropic remeshing algorithm introduced by Botsch et al [2], [4] is implemented in this package. This algorithm incrementally performs simple operations such as edge splits, edge collapses, edge flips, and Laplacian smoothing. All the vertices of the remeshed patch are reprojected to the original surface to maintain a good approximation of the input.
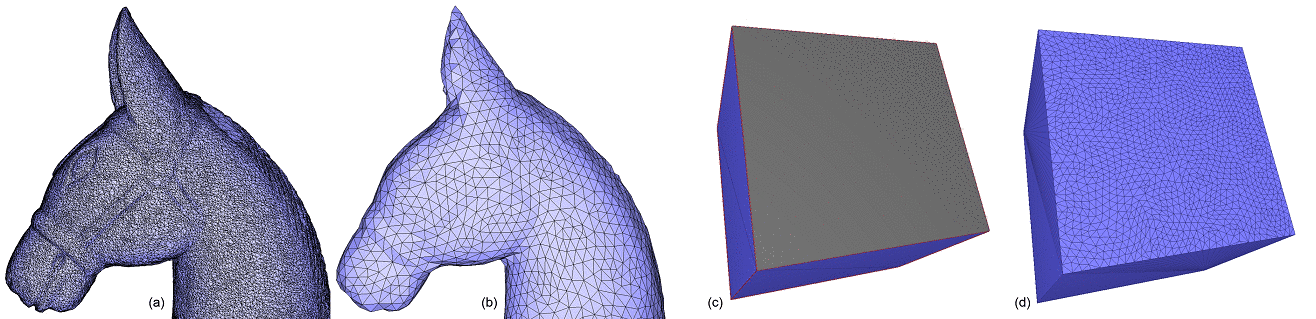
A triangulated region of a polygon mesh can be remeshed using the function CGAL::Polygon_mesh_processing::isotropic_remeshing(), as illustrated by Figure 77.2. The algorithm has two parameters: the sizing field object for the remeshed surface patch, and the number of iterations of the abovementioned sequence of operations.
As the number of iterations increases, the mesh tends to be smoother and closer to the target edge length.
The sizing field establishes the local target edge length for the remeshed surface. Two sizing fields are provided:
The distinction between uniform and adaptive sizing fields is illustrated in Figure 77.3.
An additional option allows for the protection (i.e., preservation) of specified polylines. In some cases, these polylines may be too long, making it impossible to achieve the desired target edge length while maintaining their integrity. This can lead to infinite loops of edge splits in incident faces. To avoid this, the function CGAL::Polygon_mesh_processing::split_long_edges() should be applied to the list of constrained edges prior to remeshing.
The following example demonstrates a complete usage of the isotropic remeshing function.
Example: PMP_Remeshing/isotropic_remeshing_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/boost/graph/border.h>
#include <CGAL/Polygon_mesh_processing/remesh.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <boost/iterator/function_output_iterator.hpp>
#include <iostream>
#include <string>
#include <vector>
typedef boost::graph_traits<Mesh>::halfedge_descriptor halfedge_descriptor;
typedef boost::graph_traits<Mesh>::edge_descriptor edge_descriptor;
namespace PMP = CGAL::Polygon_mesh_processing;
struct halfedge2edge
{
halfedge2edge(const Mesh& m, std::vector<edge_descriptor>& edges)
: m_mesh(m), m_edges(edges)
{}
void operator()(const halfedge_descriptor& h) const
{
m_edges.push_back(edge(h, m_mesh));
}
const Mesh& m_mesh;
std::vector<edge_descriptor>& m_edges;
};
int main(int argc, char* argv[])
{
Mesh mesh;
{
std::cerr << "Invalid input." << std::endl;
return 1;
}
double target_edge_length = (argc > 2) ? std::stod(std::string(argv[2])) : 0.04;
unsigned int nb_iter = (argc > 3) ? std::stoi(std::string(argv[3])) : 10;
std::cout << "Split border...";
std::vector<edge_descriptor> border;
std::cout << "done." << std::endl;
std::cout << "Start remeshing of " << filename << " (" << num_faces(mesh) << " faces)..." << std::endl;
CGAL::parameters::number_of_iterations(nb_iter)
.protect_constraints(true));
std::cout << "Remeshing done." << std::endl;
return 0;
}
void split_long_edges(const EdgeRange &edges, SizingFunction &sizing, PolygonMesh &pmesh, const NamedParameters &np=parameters::default_values())
splits the edges listed in edges into sub-edges that are not longer than the given threshold max_leng...
Definition: remesh.h:457
void isotropic_remeshing(const FaceRange &faces, SizingFunction &sizing, PolygonMesh &pmesh, const NamedParameters &np=parameters::default_values())
remeshes a triangulated region of a polygon mesh.
Definition: remesh.h:217
HalfedgeOutputIterator border_halfedges(const FaceRange &face_range, const Graph &g, HalfedgeOutputIterator out, const NamedParameters &np=parameters::default_values())
Approximated Discrete Centroidal Voronoi Diagram (ACVD) Remeshing
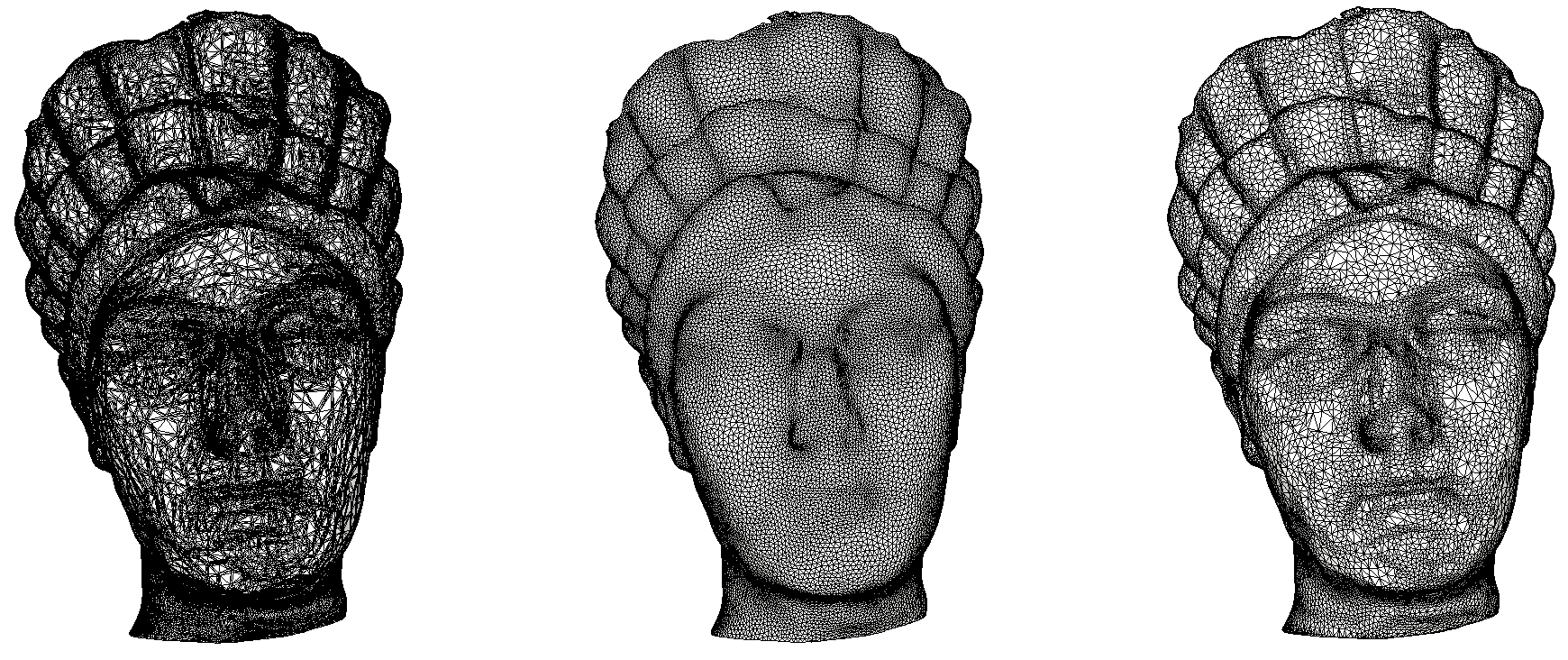
This remeshing algorithm employs clustering on polygonal meshes to approximate a Centroidal Voronoi Diagram construction. It is inspired by the method presented in [10] and further developed in [1] and [11]. The algorithm is analogous to Lloyd's algorithm (or k-means), where clusters are initialized from randomly selected input vertices and grown to minimize a specific energy function until convergence. Upon convergence, output vertices are computed from the vertices of each cluster.
The function CGAL::Polygon_mesh_processing::approximated_centroidal_Voronoi_diagram_remeshing() accepts a triangle mesh and an expected number of output vertices, updating the mesh with the remeshed result. Note that the final vertex count may exceed the input parameter if the mesh is not closed or if the specified vertex budget is insufficient to produce a manifold mesh, which may affect the uniformity of output triangles. The output mesh is not guaranteed to preserve the input topology; for example, small handles contained within a cluster may be omitted.
For meshes with sharp features or corners, quadric error metrics can be used to either move output vertices (fast, but may produce poorly shaped triangles) or to incorporate quadric error metrics directly into the cluster energy formulation (slower, but yields higher quality triangles). Adaptive remeshing based on surface curvature is also supported.
Refine and Fair
A surface patch can be refined by inserting new vertices and flipping edges to get a triangulation. Using a criterion presented in [8], the density of triangles near the boundary of the patch is approximated by the refinement function. The validity of the mesh is enforced by flipping edges. An edge is flipped only if the opposite edge does not exist in the original mesh and if no degenerate triangles are generated.
A region of the surface mesh (e.g., the refined region) can be faired to obtain a tangentially continuous and smooth surface patch. The region to be faired is defined as a set of vertices to be relocated. The fairing step minimizes a linear bi-Laplacian system with boundary constraints, as described in [3]. Visual results of these steps are shown in Figure 78.1 (c and d).
Refinement and fairing functions can be applied to arbitrary regions on a triangle mesh using:
Fairing requires a sparse linear solver; we recommend using Eigen 3.2 or later. Note that fairing may fail if the set of fixed vertices used as boundary conditions is insufficient to solve the linear system.
The following example calls the functions CGAL::Polygon_mesh_processing::refine() and CGAL::Polygon_mesh_processing::fair() for some selected regions on the input triangle mesh.
Example: PMP_Remeshing/refine_fair_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/Polygon_mesh_processing/refine.h>
#include <CGAL/Polygon_mesh_processing/fair.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <iostream>
#include <iterator>
#include <map>
#include <utility>
#include <vector>
typedef Mesh::Vertex_handle Vertex_handle;
namespace PMP = CGAL::Polygon_mesh_processing;
void extract_k_ring(Vertex_handle v,
int k,
std::vector<Vertex_handle>& qv)
{
std::map<Vertex_handle, int> D;
qv.push_back(v);
D[v] = 0;
std::size_t current_index = 0;
int dist_v;
while (current_index < qv.size() && (dist_v = D[qv[current_index]]) < k)
{
v = qv[current_index++];
Mesh::Halfedge_around_vertex_circulator e(v->vertex_begin()), e_end(e);
do {
Vertex_handle new_v = e->opposite()->vertex();
if (D.insert(std::make_pair(new_v, dist_v + 1)).second)
qv.push_back(new_v);
} while (++e != e_end);
}
}
int main(int argc, char* argv[])
{
Mesh poly;
{
std::cerr << "Invalid input." << std::endl;
return 1;
}
std::vector<Mesh::Facet_handle> new_facets;
std::vector<Vertex_handle> new_vertices;
std::back_inserter(new_facets),
std::back_inserter(new_vertices),
CGAL::parameters::density_control_factor(2.));
std::ofstream refined_off("refined.off");
refined_off.precision(17);
refined_off << poly;
refined_off.close();
std::cout << "Refinement added " << new_vertices.size() << " vertices." << std::endl;
Mesh::Vertex_iterator v = poly.vertices_begin();
std::advance(v, 82);
std::vector<Vertex_handle> region;
extract_k_ring(v, 12, region);
std::cout << "Fairing : " << (success ? "succeeded" : "failed") << std::endl;
std::ofstream faired_off("faired.off");
faired_off.precision(17);
faired_off << poly;
faired_off.close();
return 0;
}
std::pair< FaceOutputIterator, VertexOutputIterator > refine(TriangleMesh &tmesh, const FaceRange &faces, FaceOutputIterator faces_out, VertexOutputIterator vertices_out, const NamedParameters &np=parameters::default_values())
refines a region of a triangle mesh.
Definition: refine.h:78
bool fair(TriangleMesh &tmesh, const VertexRange &vertices, const NamedParameters &np=parameters::default_values())
fairs a region on a triangle mesh.
Definition: fair.h:130
Smoothing
Smoothing of a triangulated mesh region can be performed using algorithms that target either mesh smoothing or shape smoothing. Mesh smoothing improves triangle quality based on criteria such as angle and area, while shape smoothing is designed to be intrinsic, minimizing dependence on discretization and focusing on smoothing the underlying shape.
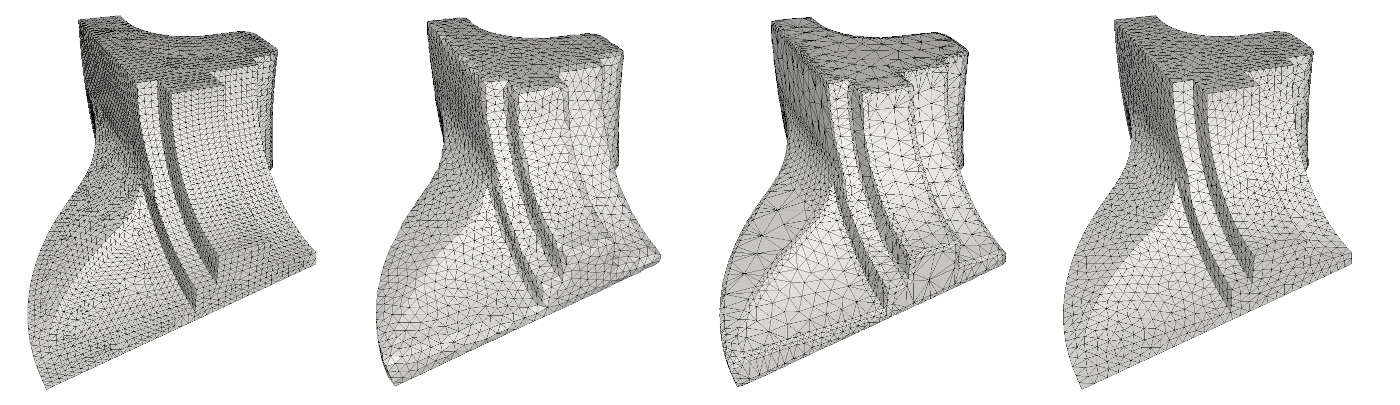
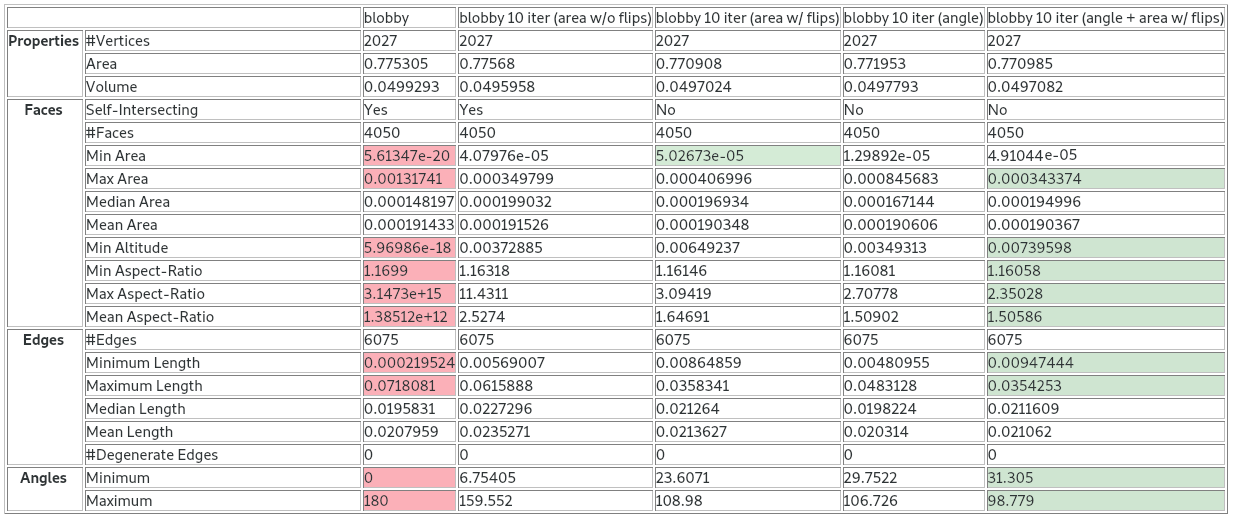
- Mesh smoothing by angle and area optimization:
CGAL::Polygon_mesh_processing::angle_and_area_smoothing() moves vertices to optimize the geometry around each vertex, aiming to equalize angles between incident edges and/or equalize areas of adjacent triangles. Border vertices are treated as constrained and remain fixed throughout the procedure. No new vertices are inserted. The algorithms are based on Surazhsky and Gotsman [9]. Area smoothing alone may produce long and skinny triangles; to mitigate this, an optional step of Delaunay-based edge flips can be applied. Area smoothing improves the spatial distribution of vertices over the smoothed region.
A simple example is provided below.
Example: PMP_Remeshing/mesh_smoothing_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/angle_and_area_smoothing.h>
#include <CGAL/Polygon_mesh_processing/detect_features.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <iostream>
#include <string>
typedef boost::graph_traits<Mesh>::edge_descriptor edge_descriptor;
namespace PMP = CGAL::Polygon_mesh_processing;
int main(int argc, char** argv)
{
Mesh mesh;
if(!PMP::IO::read_polygon_mesh(filename, mesh))
{
std::cerr << "Invalid input." << std::endl;
return EXIT_FAILURE;
}
typedef boost::property_map<Mesh, CGAL::edge_is_feature_t>::type EIFMap;
EIFMap eif = get(CGAL::edge_is_feature, mesh);
int sharp_counter = 0;
for(edge_descriptor e : edges(mesh))
if(get(eif, e))
++sharp_counter;
std::cout << sharp_counter << " sharp edges" << std::endl;
const unsigned int nb_iterations = (argc > 2) ? std::atoi(argv[2]) : 10;
std::cout << "Smoothing mesh... (" << nb_iterations << " iterations)" << std::endl;
.use_safety_constraints(false)
.edge_is_constrained_map(eif));
std::cout << "Done!" << std::endl;
return EXIT_SUCCESS;
}
void detect_sharp_edges(const PolygonMesh &pmesh, FT angle_in_deg, EdgeIsFeatureMap edge_is_feature_map, const NamedParameters &np=parameters::default_values())
void angle_and_area_smoothing(const FaceRange &faces, TriangleMesh &tmesh, const NamedParameters &np=parameters::default_values())
smooths a region of a triangle mesh.
Definition: angle_and_area_smoothing.h:137
Example: PMP_Remeshing/tangential_relaxation_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/tangential_relaxation.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <fstream>
namespace PMP = CGAL::Polygon_mesh_processing;
int main(int argc, char* argv[])
{
Mesh mesh;
{
std::cerr << "Invalid input." << std::endl;
return 1;
}
unsigned int nb_iter = (argc > 2) ? std::stoi(std::string(argv[2])) : 10;
std::cout << "Relax...";
std::cout << "done." << std::endl;
return 0;
}
void tangential_relaxation(const VertexRange &vertices, TriangleMesh &tm, const NamedParameters &np=parameters::default_values())
applies an iterative area-based tangential smoothing to the given range of vertices.
Definition: tangential_relaxation.h:134
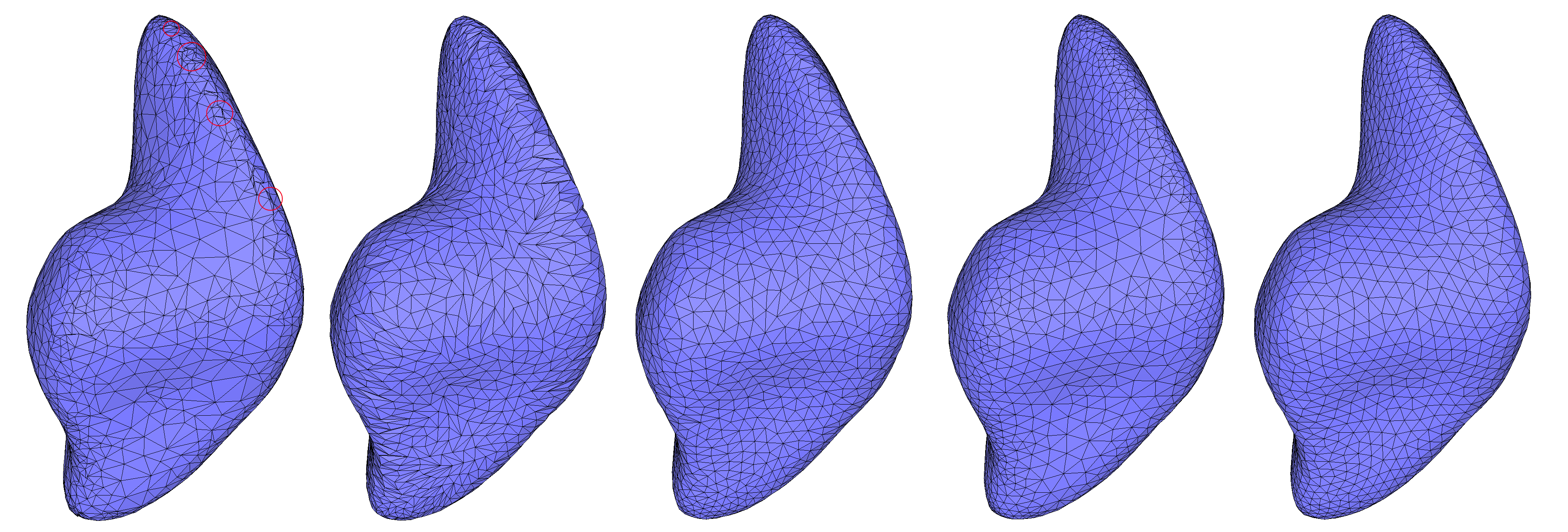
- Shape smoothing:
CGAL::Polygon_mesh_processing::smooth_shape() moves vertices towards a weighted barycenter of their neighbors along the mean curvature flow. The curvature flow algorithm for shape smoothing is based on Desbrun et al. [5] and Kazhdan et al. [7]. Vertices are translated along the surface normal at a speed proportional to the mean curvature of the region being smoothed. Vertices on sharp corners move faster, while those in flat regions remain stationary (zero curvature). To prevent undesirable neck pinches (singularities in cylindrical regions), the algorithm slows evolution in such areas. The smoothed shape converges toward a sphere while remaining conformally equivalent to its original form.
A simple example is provided below.
Example: PMP_Remeshing/shape_smoothing_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/smooth_shape.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <iostream>
#include <set>
#include <string>
namespace PMP = CGAL::Polygon_mesh_processing;
int main(int argc, char* argv[])
{
Mesh mesh;
if(!PMP::IO::read_polygon_mesh(filename, mesh))
{
std::cerr << "Invalid input." << std::endl;
return 1;
}
const unsigned int nb_iterations = (argc > 2) ? std::atoi(argv[2]) : 10;
const double time = (argc > 3) ? std::atof(argv[3]) : 0.0001;
std::set<Mesh::Vertex_index> constrained_vertices;
for(Mesh::Vertex_index v : vertices(mesh))
{
constrained_vertices.insert(v);
}
std::cout << "Constraining: " << constrained_vertices.size() << " border vertices" << std::endl;
std::cout << "Smoothing shape... (" << nb_iterations << " iterations)" << std::endl;
.vertex_is_constrained_map(vcmap));
std::cout << "Done!" << std::endl;
return EXIT_SUCCESS;
}
void smooth_shape(const FaceRange &faces, TriangleMesh &tmesh, const double time, const NamedParameters &np=parameters::default_values())
smooths the overall shape of the mesh by using the mean curvature flow.
Definition: smooth_shape.h:115
bool is_border(typename boost::graph_traits< FaceGraph >::halfedge_descriptor hd, const FaceGraph &g)
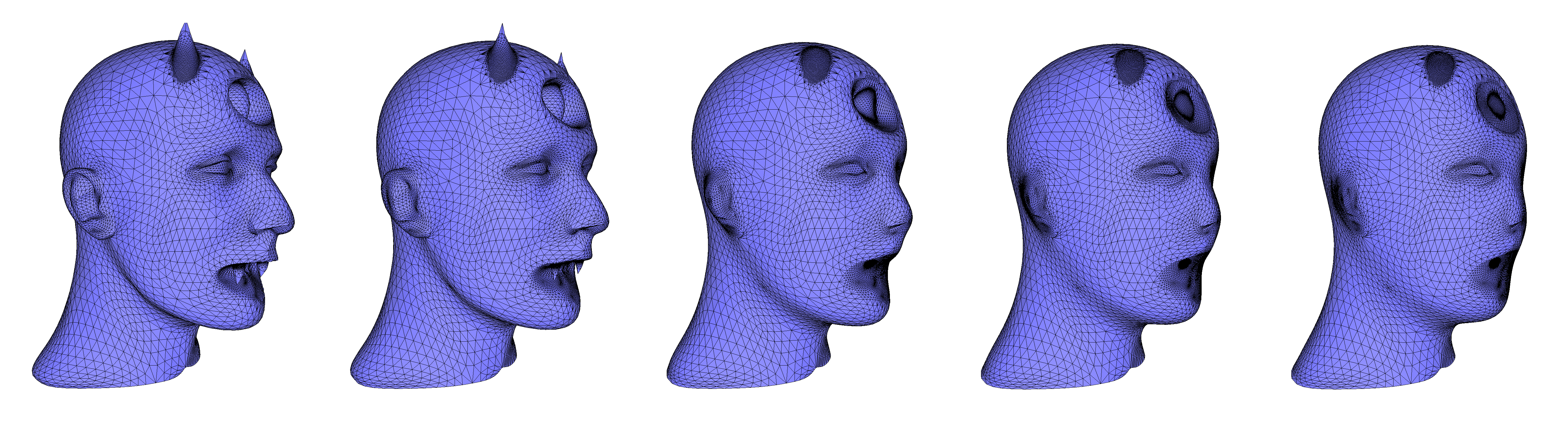
Delaunay-Based Surface Remeshing
The mesh generation algorithm implemented in the 3D Mesh Generation package can be used to remesh a given triangulated surface mesh. This algorithm, based on Delaunay refinement of a restricted Delaunay triangulation, produces a triangle surface mesh with guaranteed properties regarding simplex size, surface approximation, facet shape, and surface topology. A set of edges from the input mesh can be specified as constraints to build and protect polylines features, which are resampled while preserving the topology of the input feature graph.
This triangle surface remeshing solution is available in this package via the function CGAL::Polygon_mesh_processing::surface_Delaunay_remeshing(). All meshing criteria defined for CGAL::make_mesh_3() can be used directly, including those for simplex size, facet shape, surface approximation, topology, and one-dimensional feature sampling.
An example demonstrating remeshing of a triangulated surface mesh with the Delaunay refinement algorithm, while preserving detected sharp edges, is provided below.
Example: PMP_Remeshing/delaunay_remeshing_example.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/detect_features.h>
#include <CGAL/Polygon_mesh_processing/surface_Delaunay_remeshing.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <CGAL/Mesh_constant_domain_field_3.h>
#include <fstream>
namespace PMP = CGAL::Polygon_mesh_processing;
int main(int argc, char* argv[])
{
std::string filename = (argc > 1) ? std::string(argv[1]) :
CGAL::data_file_path(
"meshes/anchor_dense.off");
Mesh mesh;
{
std::cerr << "Invalid input." << std::endl;
return 1;
}
double target_edge_length = (argc > 2) ? std::stod(std::string(argv[2])) : 0.02;
Sizing_field size(target_edge_length);
double fdist = (argc > 3) ? std::stod(std::string(argv[3])) : 0.01;
std::cout << "Detect features..." << std::endl;
using EIFMap = boost::property_map<Mesh, CGAL::edge_is_feature_t>::type;
EIFMap eif = get(CGAL::edge_is_feature, mesh);
std::cout << "Start remeshing of " << filename << " (" << num_faces(mesh) << " faces)..." << std::endl;
.mesh_edge_size(size)
.mesh_facet_distance(fdist)
.edge_is_constrained_map(eif));
std::cout << "Remeshing done." << std::endl;
return 0;
}
TriangleMeshOut surface_Delaunay_remeshing(const TriangleMesh &tmesh, const NamedParameters &np=parameters::default_values())
remeshes a surface triangle mesh following the Delaunay refinement algorithm described in the 3D Mesh...
Definition: surface_Delaunay_remeshing.h:181
Remeshing of (Almost) Planar Patches
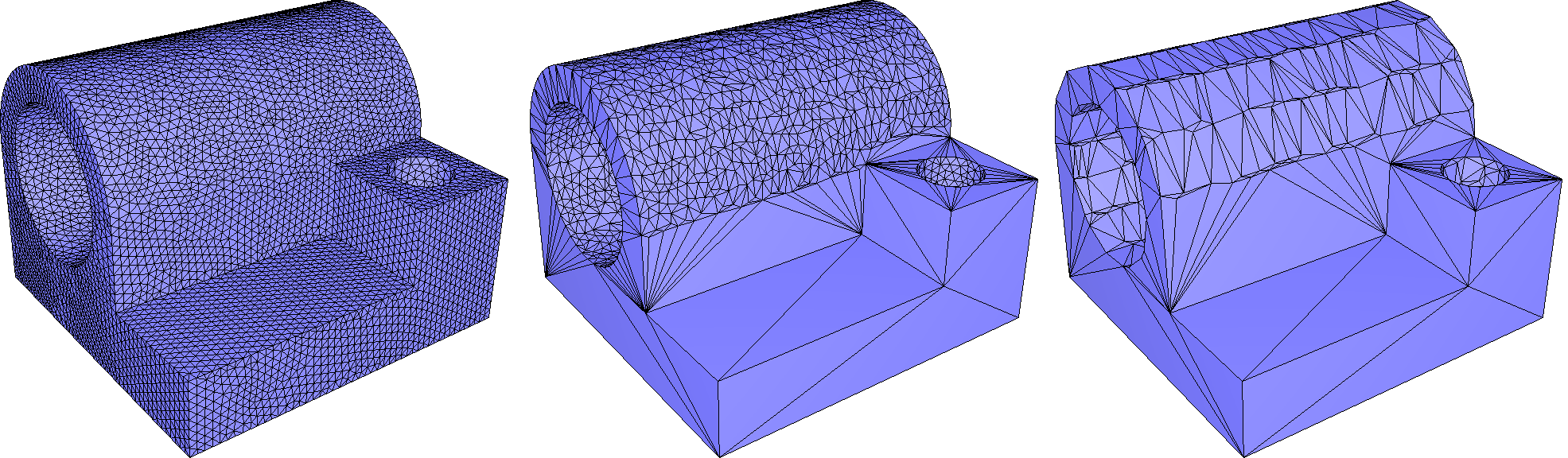
When a planar region of a model is described by many triangles, it may be desirable to simplify the mesh in this region, reducing the number of elements or even representing the region as a single large polygonal face if it forms a simply connected patch.
This can be accomplished using the function CGAL::Polygon_mesh_processing::remesh_planar_patches(), which detects planar regions using geometric predicates for coplanarity and collinearity.
Example: PMP_Remeshing/remesh_planar_patches.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/remesh_planar_patches.h>
#include <CGAL/Polygon_mesh_processing/remesh.h>
#include <CGAL/Polygon_mesh_processing/detect_features.h>
#include <CGAL/Polygon_mesh_processing/triangulate_faces.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <iostream>
#include <fstream>
namespace PMP = CGAL::Polygon_mesh_processing;
int main()
{
Mesh sm;
std::cout << "Input mesh has " << faces(sm).size() << " faces" << std::endl;
assert(faces(sm).size() == 12);
Mesh::Property_map<Mesh::Edge_index, bool> ecm =
sm.add_property_map<Mesh::Edge_index, bool>("ecm", false).first;
assert(faces(sm).size() > 100);
Mesh out;
std::cout << "Output mesh has " << faces(out).size() << " faces" << std::endl;
assert(faces(out).size() == 12);
return EXIT_SUCCESS;
}
void remesh_planar_patches(const TriangleMeshIn &tm_in, PolygonMeshOut &pm_out, const NamedParametersIn &np_in=parameters::default_values(), const NamedParametersOut &np_out=parameters::default_values())
generates a new triangle mesh pm_out with the minimal number of triangles while preserving the shape ...
Definition: remesh_planar_patches.h:1436
bool read_polygon_mesh(const std::string &fname, Graph &g, const NamedParameters &np=parameters::default_values())
Exact coplanarity and collinearity tests may result in unexpectedly small planar regions due to imperfections in the input geometry. To address this, a threshold on the angle between adjacent faces (or segments) can be specified, allowing faces to be considered coplanar (or segments collinear) within a local tolerance. However, this threshold is only local and does not provide global control, which may lead to undesired effects, such as in the case of a densely sampled circular arc where all points are eventually found to be nearly collinear.
To overcome this limitation, the function CGAL::Polygon_mesh_processing::remesh_almost_planar_patches() is provided. It expects the segmentation into planar patches and corners to be supplied by the user. Such segmentation can be obtained using CGAL::Polygon_mesh_processing::region_growing_of_planes_on_faces(), which applies a region growing algorithm to detect planar regions in a mesh using both global and local criteria.
Similarly, the function CGAL::Polygon_mesh_processing::detect_corners_of_regions() can be used to detect corner vertices on the border of the planar regions detected by running the region growing algorithm on border segments of the patch.
Example: PMP_Remeshing/remesh_almost_planar_patches.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/remesh_planar_patches.h>
#include <CGAL/Polygon_mesh_processing/region_growing.h>
#include <CGAL/Polygon_mesh_processing/IO/polygon_mesh_io.h>
#include <CGAL/Polygon_mesh_processing/random_perturbation.h>
#include <boost/property_map/vector_property_map.hpp>
#include <iostream>
#include <fstream>
namespace PMP = CGAL::Polygon_mesh_processing;
int main()
{
Mesh sm;
std::vector<std::size_t> region_ids(num_faces(sm));
std::vector<std::size_t> corner_id_map(num_vertices(sm), -1);
std::vector<bool> ecm(num_edges(sm), false);
boost::vector_property_map<CGAL::Epick::Vector_3> normal_map;
std::size_t nb_regions =
CGAL::make_random_access_property_map(region_ids),
CGAL::parameters::cosine_of_maximum_angle(0.98).
region_primitive_map(normal_map).
maximum_distance(0.011));
std::size_t nb_corners =
CGAL::make_random_access_property_map(region_ids),
nb_regions,
CGAL::make_random_access_property_map(corner_id_map),
CGAL::parameters::cosine_of_maximum_angle(0.98).
maximum_distance(0.011).
edge_is_constrained_map(CGAL::make_random_access_property_map(ecm)));
Mesh out;
out,
nb_regions, nb_corners,
CGAL::make_random_access_property_map(region_ids),
CGAL::make_random_access_property_map(corner_id_map),
CGAL::make_random_access_property_map(ecm),
CGAL::parameters::patch_normal_map(normal_map));
return 0;
}
std::size_t region_growing_of_planes_on_faces(const PolygonMesh &mesh, RegionMap region_map, const NamedParameters &np=parameters::default_values())
std::size_t detect_corners_of_regions(const PolygonMesh &mesh, RegionMap region_map, std::size_t nb_regions, CornerIdMap corner_id_map, const NamedParameters &np=parameters::default_values())
void random_perturbation(VertexRange vertices, TriangleMesh &tmesh, const double &perturbation_max_size, const NamedParameters &np=parameters::default_values())
randomly perturbs the locations of non-border vertices of a triangulated surface mesh.
Definition: random_perturbation.h:156
bool remesh_almost_planar_patches(const TriangleMeshIn &tm_in, PolygonMeshOut &pm_out, std::size_t nb_patches, std::size_t nb_corners, FacePatchMap face_patch_map, VertexCornerMap vertex_corner_map, EdgeIsConstrainedMap ecm, const NamedParametersIn &np_in=parameters::default_values(), const NamedParametersOut &np_out=parameters::default_values())
generates a new triangle mesh pm_out with the minimal number of triangles from a partition of tm_in.
Definition: remesh_planar_patches.h:1619
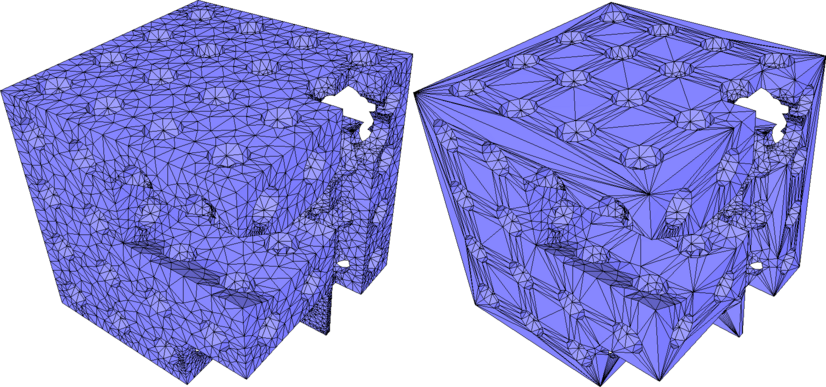 | 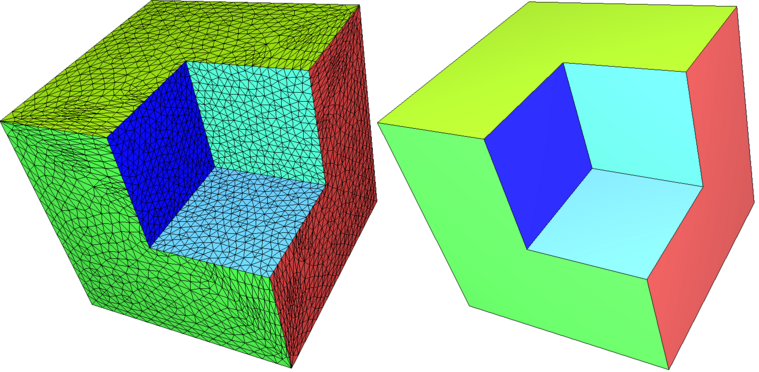 |
| (a) | (b) |
Extrusion
This package provides two functions for extruding triangle meshes with boundaries. The first extrudes by offsetting each vertex by a user-provided vector. The second is more general, accepting two user-provided functors to extrude "up" and "down". In both cases, boundaries are connected by a triangle strip. Note that extrusion may produce self-intersecting surfaces.
The following example demonstrates extrusion in both directions by projecting points along the vertex normal. If the Bottom function were the identity, this would result in a one-sided extrusion.
Example: PMP_Remeshing/extrude.cpp
Show / Hide
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Polygon_mesh_processing/compute_normal.h>
#include <CGAL/Polygon_mesh_processing/extrude.h>
#include <CGAL/IO/polygon_mesh_io.h>
#include <iostream>
#include <fstream>
#include <string>
typedef boost::graph_traits<Mesh>::vertex_descriptor vertex_descriptor;
typedef boost::property_map<Mesh, CGAL::vertex_point_t>::type VPMap;
typedef Mesh::template Property_map<vertex_descriptor, Vector> VNMap;
struct Bottom
{
Bottom(VPMap pmap, VNMap nmap, double vlen)
: pmap(pmap), nmap(nmap), vlen(vlen)
{}
void operator()(const vertex_descriptor& vin, const vertex_descriptor vout) const
{
put(pmap, vout, get(pmap, vout) - vlen* get(nmap, vin));
}
VPMap pmap;
VNMap nmap;
double vlen;
};
struct Top
{
Top(VPMap pmap, VNMap nmap, double vlen)
: pmap(pmap), nmap(nmap), vlen(vlen)
{}
void operator()(const vertex_descriptor& vin, const vertex_descriptor vout) const
{
put(pmap, vout, get(pmap, vout) + vlen* get(nmap, vin));
}
VPMap pmap;
VNMap nmap;
double vlen;
};
int main(int argc, char* argv[])
{
Mesh in, out;
std::string filename = (argc > 1) ? std::string(argv[1]) :
CGAL::data_file_path(
"meshes/cube-ouvert.off");
double vlen = (argc > 2) ? std::stod(argv[2]) : 0.1;
VNMap vnormals = in.template add_property_map<vertex_descriptor, Vector>(
"v:normal",
CGAL::NULL_VECTOR).first;
Bottom bottom(get(CGAL::vertex_point,out), vnormals, vlen);
Top top(get(CGAL::vertex_point,out), vnormals, vlen);
filename = filename.substr(filename.find_last_of("/") + 1, filename.length() - 1);
filename = filename.substr(0, filename.find_last_of("."));
filename = filename + "_" + std::to_string(vlen) + ".off";
return 0;
}
void extrude_mesh(const InputMesh &input, OutputMesh &output, const BottomFunctor &bot, const TopFunctor &top, const NamedParameters1 &np_in=parameters::default_values(), const NamedParameters2 &np_out=parameters::default_values())
performs a generalized extrusion of input and puts it in output.
Definition: extrude.h:163
void compute_vertex_normals(const PolygonMesh &pmesh, VertexNormalMap vertex_normals, const NamedParameters &np=parameters::default_values())
const CGAL::Null_vector NULL_VECTOR
Implementation History
A prototype for mesh and shape smoothing was developed during the 2017 Google Summer of Code by Konstantinos Katrioplas, supervised by Jane Tournois. It was finalized by Mael Rouxel-Labbé and integrated in CGAL 5.0.
The curvature-based sizing field for isotropic remeshing was added by Ivan Pađen during GSoC 2023, supervised by Sébastien Loriot and Jane Tournois.
The ACVD Remeshing method implementation was initiated by Hossam Saeed during GSoC 2023, supervised by Sébastien Valette and Sébastien Loriot, who later finalized the work. The implementation is based on [11] and preceding work. ACVD's implementation was also used as a reference during the project.