#include <CGAL/HDVF/Hdvf_persistence.h>

Inherits from

CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >.

Definition

template<typename CoefficientType, typename ComplexType, typename DegType, typename FiltrationType>
class CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >

The class Hdvf_persistence computes persistent homology using HDVFs.

Hence, unlike other persistence algorithms, beside standard persistent intervals informations (birth/death indices, degrees, associated cells), Hdvf_persistence also provides homology and cohomology generators for persistent pairs. Intuitively, holes die when they are "filled" by a cell: associated homology and cohomology generators provide a representation of the hole and of the cells filling the hole.

Warning: The ring of coefficients provided should actually be a field.

Given a Filtration, the Hdvf_persistence constructor basically builds a HDVF where indices of cells in the bases follow the filtration order (permutations between initial indices of cells in the chain complex and new indices given by the filtration are stored). Besides, Hdvf_persistence derives from Hdvf_core with the SparseMatrix parameter type set to Sub_sparse_matrix. Hence, Hdvf_persistence computes homology over a larger and larger sub-complex of K (encoded through a Bitboard mask of Sub_sparse_matrix) following the filtration f. At each step of the filtration, the new cell is paired (A operation) with the youngest cell valid for A.

A few words about persistent generators. At a given time \(t_2\) along the filtration, let us denote by \(\tau\) the \(q+1\)-cell inserted and let us assume that persistent homology computation pairs \(A(\sigma, \tau)\) (let \(t_1\) be the index of \(\sigma\) along the filtration). A new persistent interval \((t_1, t_2)\)is created, generated by \(\sigma\) and filled by \(\tau\). Reduction at time \(t_2-1\) (just before the insertion of \(\tau\)) provides persistent generators: \(g(\sigma)\) is a cycle and \(g(\tau)\) is a chain "filling" this cycle (before the pairing \(A(\sigma, \tau)\), the HDVF over \(K_{t_2}\) is not perfect, thus \(g(\tau)\) is not a cycle but a chain bounded by \(q\)-cycles).

Next figures illustrate such informations for a filtration of a dented double torus.

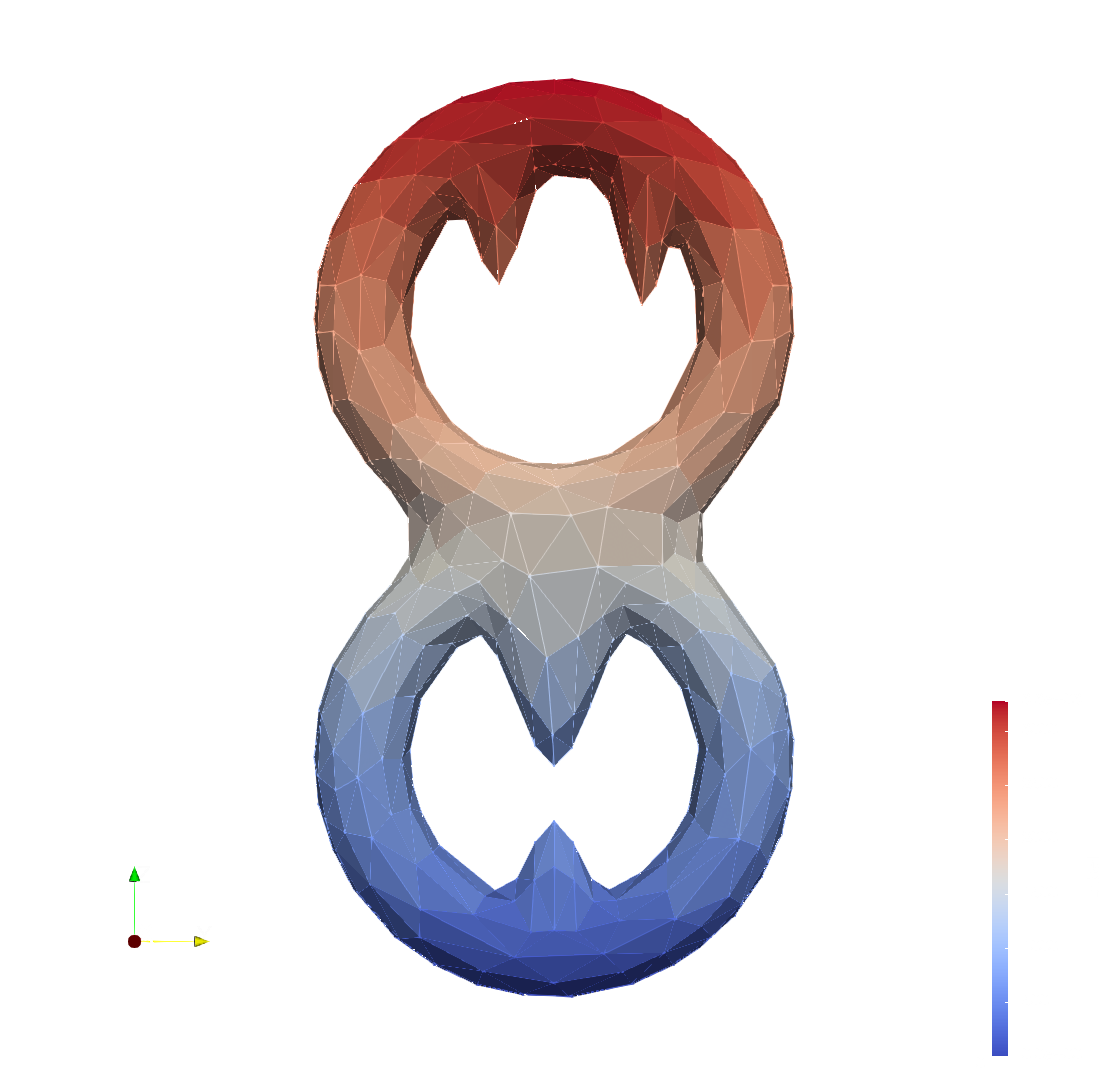
Filtration Filtration_lower_star along the z axis of a dented double torus.

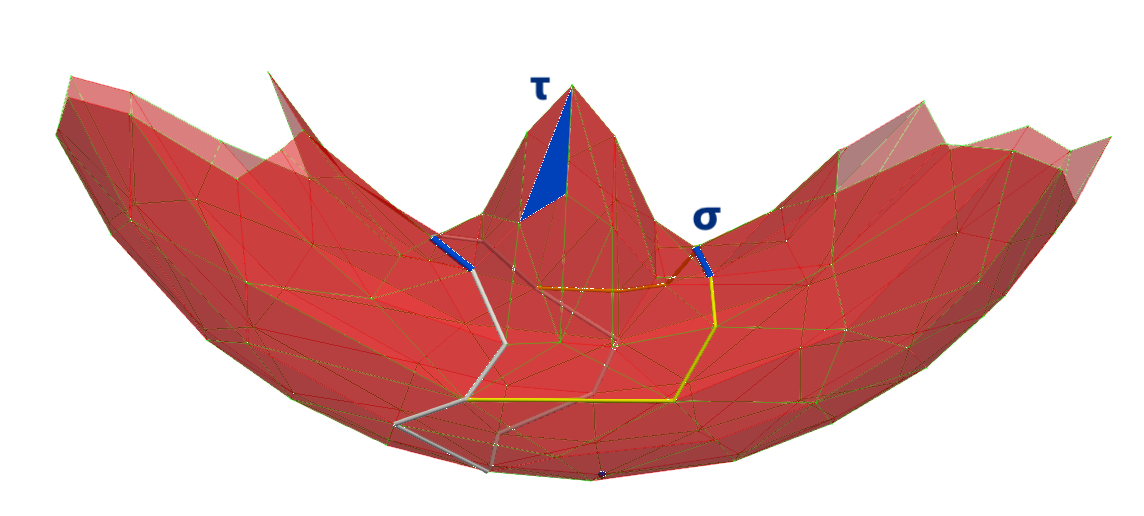
The first persistent hole is a dimension 1 hole with a duration of 0.359 along z.

(Left) the complex at time 622 along the filtration (in blue, the 2-cell \(\tau\) added at time 623). This 1-homology of this complex contains two cycles depicted in white and yellow respectively. Yellow curve: a 1-cycle born at time 319 (with cell \(\sigma\)) along the filtration. White curve: the second 1-cycle of this complex (born at time 156 along the filtration).
(Middle) the filtration adds the (blue) 2-cell \(\tau\) at time 623: this cell fills one the 1-cycles (actually the "youngest" cycle, thus the yellow one). Middle image illustrates as a yellow patch the "filling 2-chain", a chain a 2-cells filling the hole when the cell \(\tau\) is added. As stated earlier, this filling chain is not a cycle and it equals \(g(\tau)\) in the (non perfect) reduction before the pairing A(319, 623) between \(\sigma\) and \(\tau\). Middle figure illustrates that in the (non perfect) HDVF before A operation, \(g(\tau)\) is not a cycle but a chain bounded by \(q\)-cycles.
(Right) the complex after insertion of \(\tau\) and the pairing A(319, 623) between \(\sigma\) and \(\tau\). Only the white 1-cycle remains (actually its persistent lifetime is infinite).

The figure above illustrates next persistent hole (dimension 0 hole) which duration is 0.684 along z. The cell \(\tau\) is added at time 1237 and fills the 0-hole (connected component) introduced at time 756 by the cell \(\sigma\). The persistent generator associated to \(\sigma\) is simply the cell itself identifying its connected component. The persistent generator associated to \(\tau\) is a 1-chain (depicted in yellow) connecting \(\sigma\) to the critical cell identifying the second connected component.

Figures above illustrate next finite persistent intervals and (right) infinite dimension 1 persistent intervals.

Is model of: HDVF

Template Parameters

CoefficientType	a model of the `Ring` concept providing the ring used to compute homology.
ComplexType	a model of the `AbstractChainComplex` concept, providing the type of abstract chain complex used.
DegType	a scalar data type used for the degrees of the filtration.
FiltrationType	a model of the `Filtration` concept, providing the filtration used to compute persistence.

Examples: HDVF/main_per_hdvf.cpp.

Classes
struct	iterator
	Iterator over (finite) persistent intervals. More...

struct	PerIntervalInformation
	For persistent diagram iterator (returned by *it) More...

Public Types
typedef OSM::Sparse_chain< CoefficientType, OSM::COLUMN >	CChain
	Type of column-major chains.

typedef OSM::Sparse_chain< CoefficientType, OSM::ROW >	RChain
	Type of row-major chains.

typedef OSM::Sub_sparse_matrix< CoefficientType, OSM::COLUMN >	CMatrix
	Type of column-major sparse matrices.

typedef OSM::Sub_sparse_matrix< CoefficientType, OSM::ROW >	RMatrix
	Type of row-major sparse matrices.

typedef Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >	HDVFParent
	Type of parent HDVF class (Hdvf_core with appropriate template parameters) The SparseMatrix model is set to Sub_sparse_matrix to activate (co)homology computation over a subcomplex.

typedef FiltrationType	Filtration
	Type of filtrations used to compute persistence.

typedef DegreePerIntervalT< DegType >	DegreePerInterval
	Instanciation of `DegreePerIntervalT` (persistant intervals degrees) for `DegType`.

typedef PerHoleT< DegType >	PerHole
	Instanciation of `PerHoleT` (full persistant intervals informations) for `DegType`.

typedef std::vector< std::vector< int > >	ExpLabels
	Type for `PRIMARY`/`SECONDARY`/`CRITICAL` labels export Encoding used:

typedef CChain	ExpChain
	Type chains export (column-major chains)

Public Types inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >
typedef OSM::Sparse_chain< CoefficientType, OSM::COLUMN >	CChain
	Type of column-major chains.

typedef OSM::Sparse_chain< CoefficientType, OSM::ROW >	RChain
	Type of row-major chains.

typedef OSM::Sub_sparse_matrix< CoefficientType, OSM::COLUMN >	CMatrix
	Type of column-major sparse matrices.

typedef OSM::Sub_sparse_matrix< CoefficientType, OSM::ROW >	RMatrix
	Type of row-major sparse matrices.

Public Member Functions
	Hdvf_persistence (const ComplexType &K, const Filtration &f, int hdvf_opt=OPT_BND, bool with_export=false)
	Hdvf_persistence default constructor.

std::vector< PairCell >	compute_perfect_hdvf (bool verbose=false)
	Computes a perfect persistent HDVF.

bool	with_export ()
	Gets the "with_export" Boolean flag.

const Filtration &	get_filtration ()
	Get a constant reference on the filtration.

DegType	hole_duration (const PerHole hole) const
	Computes the (degree) duration of a persistent interval (ie.

ostream &	print_hdvf_persistence_info (ostream &out)
	Prints informations related to the filtration.

virtual vector< vector< int > >	get_psc_labels () const
	Exports primary/secondary/critical labels (e.g.

virtual CChain	get_homology_chain (size_t cell, int q) const
	Exports homology generators associated to `cell` (critical cell) of dimension `q` (e.g.

virtual CChain	get_cohomology_chain (size_t cell, int q) const
	Exports cohomology generators associated to `cell` (critical cell) of dimension `q` (used by vtk export).

iterator	begin (bool discard_small=true)
	Iterator to the beginning of persistent intervals.

iterator	end ()
	Iterator to the ending of the chains indices.

Public Member Functions inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >
	Hdvf_core (const ComplexType &K, int hdvf_opt=OPT_FULL)
	Default constructor.

	Hdvf_core (const Hdvf_core &hdvf)

	~Hdvf_core ()

virtual PairCell	find_pair_A (int q, bool &found) const
	Finds a valid PairCell of dimension q / q+1 for A.

virtual PairCell	find_pair_A (int q, bool &found, size_t gamma) const
	Finds a valid PairCell for A containing `gamma` (a cell of dimension `q`)

virtual std::vector< PairCell >	find_pairs_A (int q, bool &found) const
	Finds all valid PairCell of dimension q / q+1 for A.

virtual std::vector< PairCell >	find_pairs_A (int q, bool &found, size_t gamma) const
	Finds all valid PairCell for A containing `gamma` (a cell of dimension `q`)

void	A (size_t gamma1, size_t gamma2, int q)
	A operation: pairs critical cells.

std::vector< PairCell >	compute_perfect_hdvf (bool verbose=false)
	Computes a perfect HDVF.

std::vector< PairCell >	compute_rand_perfect_hdvf (bool verbose=false)
	Computes a random perfect HDVF.

bool	is_perfect_hdvf ()
	Tests if a HDVF is perfect.

virtual std::vector< std::vector< size_t > >	get_flag (FlagType flag) const
	Gets cells with a given `flag` in any dimension.

virtual std::vector< size_t >	get_flag_dim (FlagType flag, int q) const
	Gets cells with a given `flag` in dimension `q`.

FlagType	get_cell_flag (int q, size_t tau) const
	Gets the flag of the cell `tau` in dimension `q`.

int	get_hdvf_opts () const
	Gets HDVF computation option.

const RMatrix &	get_f (int q) const
	Gets the row-major matrix of \(f\) (from the reduction associated to the HDVF).

const CMatrix &	get_g (int q) const
	Gets the column-major matrix of \(g\) (from the reduction associated to the HDVF).

const CMatrix &	get_h (int q) const
	Gets the column-major matrix of \(h\) (from the reduction associated to the HDVF).

const CMatrix &	get_dd (int q) const
	Gets the column-major matrix of \(\partial'\), reduced boundary operator (from the reduction associated to the HDVF).

std::ostream &	print_matrices (std::ostream &out=std::cout) const
	Prints the matrices of the reduction.

std::ostream &	print_reduction (std::ostream &out=std::cout) const
	Prints the homology and cohomology reduction information.

virtual std::vector< std::vector< int > >	get_psc_labels () const
	Exports primary/secondary/critical labels (in particular for vtk export)

virtual CChain	get_homology_chain (size_t cell, int q) const
	Gets homology generators associated to `cell` (critical cell) of dimension `q` (used by vtk export).

virtual CChain	get_cohomology_chain (size_t cell, int dim) const
	Gets cohomology generators associated to `cell` (critical cell) of dimension `q` (used by vtk export).

std::ostream &	save_hdvf_reduction (std::ostream &out)
	Saves a HDVF together with the associated reduction (f, g, h, d matrices)

std::istream &	load_hdvf_reduction (std::istream &out)
	Loads a HDVF together with the associated reduction (f, g, h, d matrices)

Protected Attributes
const Filtration &	_f

std::vector< std::vector< size_t > >	_K_to_per

std::vector< std::vector< size_t > >	_per_to_K

std::vector< PerHole >	_persist

bool	_with_export

std::vector< ExpLabels >	_export_labels

std::vector< std::pair< ExpChain, ExpChain > >	_export_g

std::vector< std::pair< ExpChain, ExpChain > >	_export_fstar

size_t	_t

std::vector< size_t >	_t_dim

std::vector< OSM::Bitboard >	_masks

Protected Attributes inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >
std::vector< std::vector< FlagType > >	_flag

std::vector< size_t >	_nb_P

std::vector< size_t >	_nb_S

std::vector< size_t >	_nb_C

std::vector< RMatrix >	_F_row

std::vector< CMatrix >	_G_col

std::vector< CMatrix >	_H_col

std::vector< CMatrix >	_DD_col

const ComplexType &	_K

int	_hdvf_opt

Friends
ostream &	operator<< (ostream &out, const Hdvf_persistence &per_hdvf)
	Overload of operator<< for Hdvf_persistence.

Additional Inherited Members
Protected Member Functions inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >
OSM::Sparse_chain< CoefficientType, ChainTypeFlag >	projection (const OSM::Sparse_chain< CoefficientType, ChainTypeFlag > &chain, FlagType flag, int q) const

void	progress_bar (size_t i, size_t n)

Member Typedef Documentation

◆ ExpLabels

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

typedef std::vector<std::vector<int> > CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::ExpLabels

Type for PRIMARY/SECONDARY/CRITICAL labels export Encoding used:

PRIMARY: -1
SECONDARY: +1
CRITICAL: 0

Constructor & Destructor Documentation

◆ Hdvf_persistence()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::Hdvf_persistence	(	const ComplexType &	K,
		const Filtration &	f,
		int	hdvf_opt = `OPT_BND`,
		bool	with_export = `false`
	)

Hdvf_persistence default constructor.

Builds an "empty" HDVF_persistence (with all cells critical) associated to the chain complex K and the filtration f. By default, the HDVF option is set to OPT_FULL (full reduction computed)

Parameters

[in]	K	A chain complex (a model of `AbstractChainComplex`).
[in]	f	A filtration (a model of `Filtration`).
[in]	hdvf_opt	Option for HDVF computation (`OPT_BND`, `OPT_F`, `OPT_G` or `OPT_FULL`)
[in]	with_export	Boolean option to activate or not the export of PSC labels and homology/cohomology generators for of persistent intervals of positive duration. This information is used by vtk exporters.

Member Function Documentation

◆ begin()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

iterator CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::begin ( bool discard_small = true )

Iterator to the beginning of persistent intervals.

Parameters

[in] discard_small If true, the iterator visits only persistent intervals of (strictly) positive degree duration. Otherwise, visit all persistent intervals.

Returns: The iterator to the beginning of the chains indices.

◆ compute_perfect_hdvf()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

std::vector< PairCell > CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::compute_perfect_hdvf ( bool verbose = false )

Computes a perfect persistent HDVF.

This method follows the filtration and considers cells one by one. For each of them, it searches the youngest possible cell valid for A (returned by find_pair_A()), and applies the corresponding A() operation. By definition of persistent homology, the Ring of coefficients must be a field.

Parameters

[in] verbose If this parameter is true, all intermediate reductions are printed out.

Returns: The vector of all PairCell paired with A.

◆ end()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

iterator CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::end ( )

Iterator to the ending of the chains indices.

Returns: The iterator to the ending of the chains indices.

◆ get_cohomology_chain()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

virtual CChain CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::get_cohomology_chain	(	size_t	cell,
		int	q
	)		const

virtual

Exports cohomology generators associated to cell (critical cell) of dimension q (used by vtk export).

The method exports the chain \(f^\star(\sigma)\) for \(\sigma\) the cell of index cell and dimension q.

Returns: A column-major chain.

Reimplemented from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >.

◆ get_homology_chain()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

virtual CChain CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::get_homology_chain	(	size_t	cell,
		int	q
	)		const

virtual

Exports homology generators associated to cell (critical cell) of dimension q (e.g.

forx@ vtk export).

The method exports the chain \(g(\sigma)\) for \(\sigma\) the cell of index cell and dimension q.

Returns: A column-major chain.

Reimplemented from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >.

◆ get_psc_labels()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

virtual vector< vector< int > > CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::get_psc_labels ( ) const

virtual

Exports primary/secondary/critical labels (e.g.

for vtk export).

The method exports the labels of every cells in each dimension. Encoding used:

PRIMARY: -1
SECONDARY: +1
CRITICAL: 0

Returns: A vector containing, for each dimension, the vector of labels by cell index.

Reimplemented from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sub_sparse_matrix >.

◆ hole_duration()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

DegType CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::hole_duration ( const PerHole hole ) const

Computes the (degree) duration of a persistent interval (ie.

persistent hole)

By definitions of "default" values, infinite intervals have a duration of -1.

Parameters

[in] hole Persistent interval considered for duration computation

◆ print_hdvf_persistence_info()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

ostream & CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::print_hdvf_persistence_info ( ostream & out )

Prints informations related to the filtration.

Prints out the filtration and associated permutations (_K_to_per and _per_to_K) between indices of cells in each dimension in the basis of K and indices along the filtration.

Parameters

[in] out Reference to an out stream.

◆ with_export()

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

bool CGAL::HDVF::Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType >::with_export ( )

Gets the "with_export" Boolean flag.

If the flag is true, homology/cohomology generators and corresponding PSC labels are exported for each persistent interval of positive duration.

Friends And Related Function Documentation

◆ operator<<

template<typename CoefficientType , typename ComplexType , typename DegType , typename FiltrationType >

ostream & operator<<	(	ostream &	out,
		const Hdvf_persistence< CoefficientType, ComplexType, DegType, FiltrationType > &	per_hdvf
	)

friend

Overload of operator<< for Hdvf_persistence.

Prints out finite and infinite persistence intervals.

Parameters

[in]	out	Reference to an out stream.
[in]	per_hdvf	Constant reference on the Hdvf_persistence to print.

Inherits from

Definition

Classes

Public Types

Public Member Functions

Protected Attributes

Friends

Additional Inherited Members

Member Typedef Documentation

◆ ExpLabels

Constructor & Destructor Documentation

◆ Hdvf_persistence()

Member Function Documentation

◆ begin()

◆ compute_perfect_hdvf()

◆ end()

◆ get_cohomology_chain()

◆ get_homology_chain()

◆ get_psc_labels()

◆ hole_duration()

◆ print_hdvf_persistence_info()

◆ with_export()

Friends And Related Function Documentation

◆ operator<<