#include <CGAL/HDVF/Hdvf.h>

Inherits from

CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sparse_matrix >.

Definition

template<typename CoefficientType, typename ComplexType>
class CGAL::HDVF::Hdvf< CoefficientType, ComplexType >

The class Hdvf implements homology and cohomology computation via homological discrete vector fields (HDVF for short).

It derives from Hdvf_core and shares all its data and methods.

But besides construction operations and methods (using the A() operation), the Hdvf class implements four other HDVF operations: R, M, W and MW together with appropriate "find_pair()" functions. These operations change the HDVF (that is change homology / cohomology generators) and thus provide a convenient tool to move inside the "space of homology/cohomology computations".

R() operation is the "dual" of the A pairing operation (it cancels the pairing and turns back a PRIMARY/SECONDARY pair into a pair of CRITICAL cells)
M() operation exchanges a PRIMARY \(\pi\) and a CRITICAL cell \(\gamma\) (under conditions) and modifies the homology generator associated to \(\gamma\) (while preserving is associated cohomology generator)
W() operation exchanges a SECONDARY \(\sigma\) and a CRITICAL cell \(\gamma\) (under conditions) and modifies the cohomology generator associated to \(\gamma\) (while preserving is associated homology generator)
MW() operation exchanges a PRIMARY \(\pi\) and a SECONDARY cell \(\sigma\) (under conditions). See the introduction to HDVF for more details on this operation.

Using appropriate combinations of such operations, one can change a HDVF until corresponding homology or cohomology generators meet a given basis or delineate a hole.

Let us consider the following simple cubical complex and a perfect HDVF (top) together with the three corresponding homology generators (bottom, highlighted in pink):

A W operation between cells of Khalimsky coordinates \(\sigma = (3,2)\) (CRITICAL) and \(\tau=(5,2)\) (SECONDARY) produces the following HDVF (homology generators did not change; note that cohomology generators are modified):

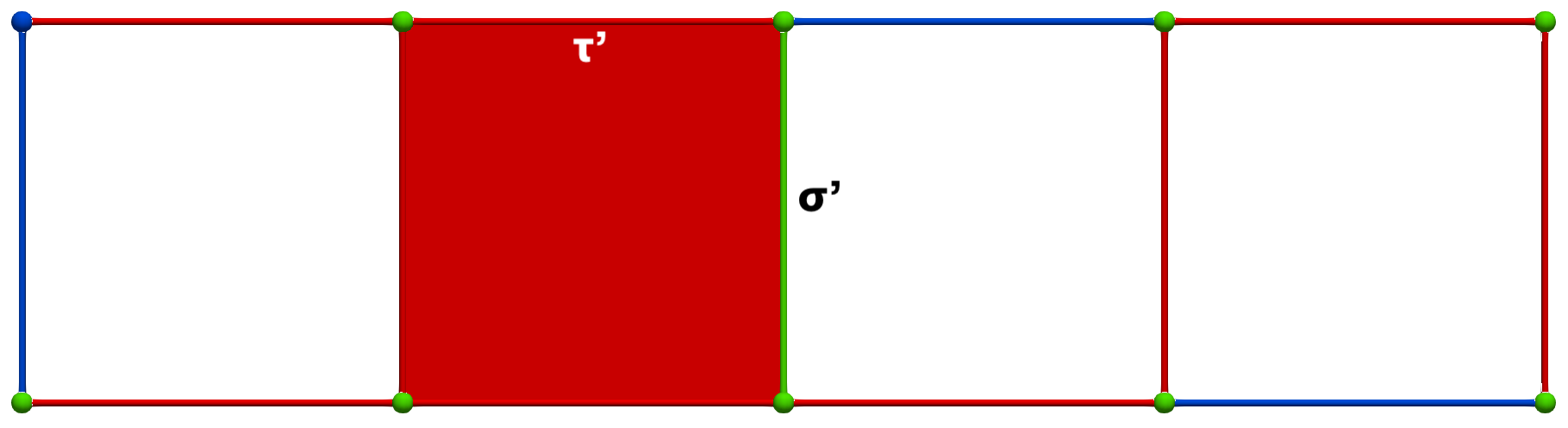
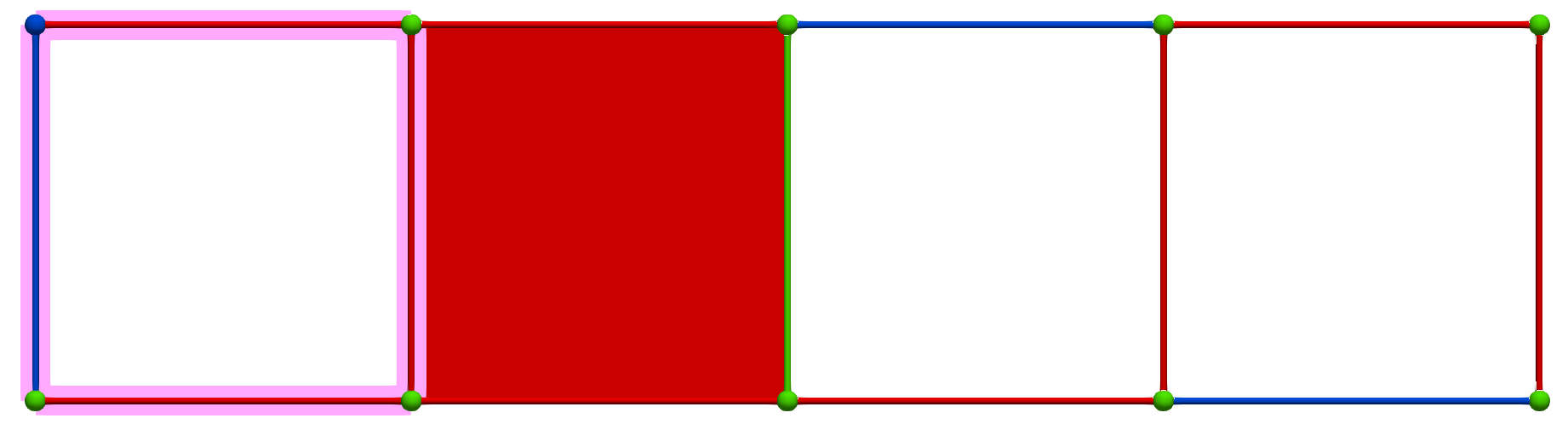
Then, a MW operation between cells of Khalimsky coordinates \(\sigma' = (4,1)\) (PRIMARY) and \(\tau=(3,2)\) (SECONDARY) produces the following HDVF where homology generators become "minimal":

Perfect HDVFs provide various topological results:

Betti numbers: are well known topological descriptors (providing the number of holes in each dimension). For a perfect HDVF, Betti numbers equal the number of critical cells (that can be obtained through get_flag() or get_flag_dim() with the CRITICAL flag as argument).
Homology/cohomology generators are actually algebraic objects, namely chains. Methods get_homology_chain() and get_cohomology_chain() return the homology and cohomology generator chain associated to a given critical cell. VTK export functions output all the cells of such chains with non zero coefficients. Figures here above illustrate such homology and co-homology generators.
Homology/cohomology annotation: use get_annotation() or get_coannotation() to get the annotation/co-annotation of a cycle/co-cycle in the homology/cohomology basis (as a chain of critical cells).
Homology/cohomology comparison: use are_same_cycles() or are_same_cocycles() to check if two cycles (or co-cycles) belong to the same homology / cohomology class.

Figure 92.1 Illustration of cycles annotation and comparison. Left: Generator \(g(\sigma)\) associated to the critical cell \(\sigma\); Middle: A cycle \(\alpha\) ; Right: A second cycle \(\beta\).

For \(\mathbb Z_2\) homology, the annotation of \(\alpha\) is \(\sigma\) ( \(\alpha\) equals \(g(\sigma)\) up to a boundary), while the annotation of \(\beta\) is \(\sigma+\tau+\gamma\) ( \(\beta\) equals \(g(\sigma)+g(\tau)+g(\gamma)\) up to a boundary).

Therefore, are_same_cycles will return true for \(\alpha\) and \(g(\sigma)\), but false for \(\beta\) and \(g(\sigma)\).

Is model of: HDVF

Template Parameters

CoefficientType	a model of the `Ring` concept providing the ring used to compute homology.
ComplexType	a model of the `AbstractChainComplex` concept, providing the type of abstract chain complex used.

Examples: HDVF/example_hdvf_cubical.cpp, HDVF/example_hdvf_simplicial.cpp, and HDVF/main_hdvf.cpp.

Public Types
typedef Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sparse_matrix >	HDVF_coreT
	Type of parent Hdvf_core class.

Public Types inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sparse_matrix >
typedef OSM::Sparse_chain< CoefficientType, OSM::COLUMN >	CChain
	Type of column-major chains.

typedef OSM::Sparse_chain< CoefficientType, OSM::ROW >	RChain
	Type of row-major chains.

typedef OSM::Sparse_matrix< CoefficientType, OSM::COLUMN >	CMatrix
	Type of column-major sparse matrices.

typedef OSM::Sparse_matrix< CoefficientType, OSM::ROW >	RMatrix
	Type of row-major sparse matrices.

Public Member Functions
	Hdvf (const ComplexType &K, int hdvf_opt=OPT_FULL)
	Default constructor.

	Hdvf (const Hdvf &hdvf)

	~Hdvf ()

PairCell	find_pair_M (int q, bool &found) const
	Finds a valid PairCell of dimension q for M.

PairCell	find_pair_M (int q, bool &found, size_t tau) const
	Finds a valid PairCell of dimension q for M cointaining `tau`.

std::vector< PairCell >	find_pairs_M (int q, bool &found) const
	Finds all valid PairCell of dimension q for M.

std::vector< PairCell >	find_pairs_M (int q, bool &found, size_t tau) const
	Finds all valid PairCell of dimension q for M cointaining `tau`.

PairCell	find_pair_W (int q, bool &found) const
	Finds a valid PairCell of dimension q for W.

PairCell	find_pair_W (int q, bool &found, size_t tau) const
	Finds a valid PairCell of dimension q for W cointaining `tau`.

std::vector< PairCell >	find_pairs_W (int q, bool &found) const
	Finds all valid PairCell of dimension q for W.

std::vector< PairCell >	find_pairs_W (int q, bool &found, size_t tau) const
	Finds all valid PairCell of dimension q for W cointaining `tau`.

PairCell	find_pair_MW (int q, bool &found) const
	Finds a valid PairCell of dimension q for MW.

PairCell	find_pair_MW (int q, bool &found, size_t tau) const
	Finds a valid PairCell of dimension q for MW cointaining `tau`.

std::vector< PairCell >	find_pairs_MW (int q, bool &found) const
	Finds all valid PairCell of dimension q for MW.

std::vector< PairCell >	find_pairs_MW (int q, bool &found, size_t tau) const
	Finds all valid PairCell of dimension q for W cointaining `tau`.

void	R (size_t pi, size_t sigma, int q)
	R operation (cancels a A operation).

void	M (size_t pi, size_t gamma, int q)
	M operation.

void	W (size_t sigma, size_t gamma, int q)
	W operation.

void	MW (size_t pi, size_t sigma, int q)
	MW operation.

HDVF_coreT::CChain	get_annotation (typename HDVF_coreT::CChain chain, int dim) const
	Gets the annotation of a cycle in the homology basis.

HDVF_coreT::RChain	get_coannotation (typename HDVF_coreT::RChain chain, int dim) const
	Gets the co-annotation of a co-cycle in the cohomology basis.

bool	are_same_cycles (HDVF_coreT::CChain chain1, HDVF_coreT::CChain chain2, int dim)
	Checks if two cycles belong to the same homology class.

bool	are_same_cocycles (HDVF_coreT::RChain chain1, HDVF_coreT::RChain chain2, int dim)
	Checks if two co-cycles belong to the same cohomology class.

Public Member Functions inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sparse_matrix >
	Hdvf_core (const ComplexType &K, int hdvf_opt=OPT_FULL)
	Default constructor.

	Hdvf_core (const Hdvf_core &hdvf)

	~Hdvf_core ()

virtual PairCell	find_pair_A (int q, bool &found) const
	Finds a valid PairCell of dimension q / q+1 for A.

virtual PairCell	find_pair_A (int q, bool &found, size_t gamma) const
	Finds a valid PairCell for A containing `gamma` (a cell of dimension `q`)

virtual std::vector< PairCell >	find_pairs_A (int q, bool &found) const
	Finds all valid PairCell of dimension q / q+1 for A.

virtual std::vector< PairCell >	find_pairs_A (int q, bool &found, size_t gamma) const
	Finds all valid PairCell for A containing `gamma` (a cell of dimension `q`)

void	A (size_t gamma1, size_t gamma2, int q)
	A operation: pairs critical cells.

std::vector< PairCell >	compute_perfect_hdvf (bool verbose=false)
	Computes a perfect HDVF.

std::vector< PairCell >	compute_rand_perfect_hdvf (bool verbose=false)
	Computes a random perfect HDVF.

bool	is_perfect_hdvf ()
	Tests if a HDVF is perfect.

virtual std::vector< std::vector< size_t > >	get_flag (FlagType flag) const
	Gets cells with a given `flag` in any dimension.

virtual std::vector< size_t >	get_flag_dim (FlagType flag, int q) const
	Gets cells with a given `flag` in dimension `q`.

FlagType	get_cell_flag (int q, size_t tau) const
	Gets the flag of the cell `tau` in dimension `q`.

int	get_hdvf_opts () const
	Gets HDVF computation option.

const RMatrix &	get_f (int q) const
	Gets the row-major matrix of \(f\) (from the reduction associated to the HDVF).

const CMatrix &	get_g (int q) const
	Gets the column-major matrix of \(g\) (from the reduction associated to the HDVF).

const CMatrix &	get_h (int q) const
	Gets the column-major matrix of \(h\) (from the reduction associated to the HDVF).

const CMatrix &	get_dd (int q) const
	Gets the column-major matrix of \(\partial'\), reduced boundary operator (from the reduction associated to the HDVF).

std::ostream &	print_matrices (std::ostream &out=std::cout) const
	Prints the matrices of the reduction.

std::ostream &	print_reduction (std::ostream &out=std::cout) const
	Prints the homology and cohomology reduction information.

virtual std::vector< std::vector< int > >	get_psc_labels () const
	Exports primary/secondary/critical labels (in particular for vtk export)

virtual CChain	get_homology_chain (size_t cell, int q) const
	Gets homology generators associated to `cell` (critical cell) of dimension `q` (used by vtk export).

virtual CChain	get_cohomology_chain (size_t cell, int dim) const
	Gets cohomology generators associated to `cell` (critical cell) of dimension `q` (used by vtk export).

std::ostream &	save_hdvf_reduction (std::ostream &out)
	Saves a HDVF together with the associated reduction (f, g, h, d matrices)

std::istream &	load_hdvf_reduction (std::istream &out)
	Loads a HDVF together with the associated reduction (f, g, h, d matrices)

Additional Inherited Members
Protected Member Functions inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sparse_matrix >
OSM::Sparse_chain< CoefficientType, ChainTypeFlag >	projection (const OSM::Sparse_chain< CoefficientType, ChainTypeFlag > &chain, FlagType flag, int q) const

void	progress_bar (size_t i, size_t n)

Protected Attributes inherited from CGAL::HDVF::Hdvf_core< CoefficientType, ComplexType, OSM::Sparse_chain, OSM::Sparse_matrix >
std::vector< std::vector< FlagType > >	_flag

std::vector< size_t >	_nb_P

std::vector< size_t >	_nb_S

std::vector< size_t >	_nb_C

std::vector< RMatrix >	_F_row

std::vector< CMatrix >	_G_col

std::vector< CMatrix >	_H_col

std::vector< CMatrix >	_DD_col

const ComplexType &	_K

int	_hdvf_opt

Constructor & Destructor Documentation

◆ Hdvf()

template<typename CoefficientType , typename ComplexType >

CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::Hdvf	(	const ComplexType &	K,
		int	hdvf_opt = `OPT_FULL`
	)

Default constructor.

Builds a "empty" HDVF associated to K (with all cells critical). By default, the HDVF option is set to OPT_FULL (full reduction computed).

Parameters

[in]	K	A chain complex (a model of `AbstractChainComplex`)
[in]	hdvf_opt	Option for HDVF computation (`OPT_BND`, `OPT_F`, `OPT_G` or `OPT_FULL`)

Member Function Documentation

◆ are_same_cocycles()

template<typename CoefficientType , typename ComplexType >

bool CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::are_same_cocycles	(	HDVF_coreT::RChain	chain1,
		HDVF_coreT::RChain	chain2,
		int	dim
	)

Checks if two co-cycles belong to the same cohomology class.

Warning: Will raise an error is chains provided are not co-cycles.; The HDVF must be perfect.

Parameters

[in]	chain1	First co-cycle.
[in]	chain2	Second co-cycle.
[in]	dim	Dimension of both co-cycles.

◆ are_same_cycles()

template<typename CoefficientType , typename ComplexType >

bool CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::are_same_cycles	(	HDVF_coreT::CChain	chain1,
		HDVF_coreT::CChain	chain2,
		int	dim
	)

Checks if two cycles belong to the same homology class.

Warning: Will raise an error is chains provided are not cycles.; The HDVF must be perfect.

Parameters

[in]	chain1	First cycle.
[in]	chain2	Second cycle.
[in]	dim	Dimension of both cycles.

◆ find_pair_M() [1/2]

template<typename CoefficientType , typename ComplexType >

PairCell CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pair_M	(	int	q,
		bool &	found
	)		const

Finds a valid PairCell of dimension q for M.

The function searches a pair of cells \((\pi, \gamma)\) with \(\pi\) PRIMARY and \(\gamma\) CRITICAL, valid for M (ie. such that \(\langle f(\pi), \gamma \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pair_M() [2/2]

template<typename CoefficientType , typename ComplexType >

PairCell CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pair_M	(	int	q,
		bool &	found,
		size_t	tau
	)		const

Finds a valid PairCell of dimension q for M cointaining tau.

The function searches a pair of cells \((\pi, \gamma)\) with \(\pi\) PRIMARY and \(\gamma\) CRITICAL (one of them is tau), valid for M (ie. such that \(\langle f(\pi), \gamma \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
[in]	tau	Cell of dimension `q` to pair.

◆ find_pair_MW() [1/2]

template<typename CoefficientType , typename ComplexType >

PairCell CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pair_MW	(	int	q,
		bool &	found
	)		const

Finds a valid PairCell of dimension q for MW.

The function searches a pair of cells \((\pi, \sigma)\) with \(\pi\) PRIMARY and \(\sigma\) SECONDARY, valid for MW (ie. such that \(\langle h_{q-1}\partial_q(\pi), \sigma \rangle\) invertible and \(\langle \partial_{q+1} h_q(\sigma), \pi \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pair_MW() [2/2]

template<typename CoefficientType , typename ComplexType >

PairCell CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pair_MW	(	int	q,
		bool &	found,
		size_t	tau
	)		const

Finds a valid PairCell of dimension q for MW cointaining tau.

The function searches a pair of cells \((\pi, \sigma)\) with \(\pi\) PRIMARY and \(\sigma\) SECONDARY (one of them is tau), valid for MW (ie. such that \(\langle h_{q-1}\partial_q(\pi), \sigma \rangle\) invertible and \(\langle \partial_{q+1} h_q(\sigma), \pi \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
[in]	tau	Cell of dimension `q` to pair.

◆ find_pair_W() [1/2]

template<typename CoefficientType , typename ComplexType >

PairCell CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pair_W	(	int	q,
		bool &	found
	)		const

Finds a valid PairCell of dimension q for W.

The function searches a pair of cells \((\sigma, \gamma)\) with \(\sigma\) SECONDARY and \(\gamma\) CRITICAL, valid for W (ie. such that \(\langle g(\gamma), \sigma \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pair_W() [2/2]

template<typename CoefficientType , typename ComplexType >

PairCell CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pair_W	(	int	q,
		bool &	found,
		size_t	tau
	)		const

Finds a valid PairCell of dimension q for W cointaining tau.

The function searches a pair of cells \((\sigma, \gamma)\) with \(\sigma\) SECONDARY and \(\gamma\) CRITICAL (one of them is tau), valid for W (ie. such that \(\langle g(\gamma), \sigma \rangle\) invertible). It returns the first valid pair found by iterators.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
[in]	tau	Cell of dimension `q` to pair.

◆ find_pairs_M() [1/2]

template<typename CoefficientType , typename ComplexType >

std::vector< PairCell > CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pairs_M	(	int	q,
		bool &	found
	)		const

Finds all valid PairCell of dimension q for M.

The function searches all pairs of cells \((\pi, \gamma)\) with \(\pi\) PRIMARY and \(\gamma\) CRITICAL, valid for M (ie. such that \(\langle f(\pi), \gamma \rangle\) invertible). It returns a vector of such pairs.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pairs_M() [2/2]

template<typename CoefficientType , typename ComplexType >

std::vector< PairCell > CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pairs_M	(	int	q,
		bool &	found,
		size_t	tau
	)		const

Finds all valid PairCell of dimension q for M cointaining tau.

The function searches all pairs of cells \((\pi, \gamma)\) with \(\pi\) PRIMARY and \(\gamma\) CRITICAL (one of them is tau), valid for M (ie. such that \(\langle f(\pi), \gamma \rangle\) invertible). It returns a vector of such pairs.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
[in]	tau	Cell of dimension `q` to pair.

◆ find_pairs_MW() [1/2]

template<typename CoefficientType , typename ComplexType >

std::vector< PairCell > CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pairs_MW	(	int	q,
		bool &	found
	)		const

Finds all valid PairCell of dimension q for MW.

The function searches all pairs of cells \((\pi, \sigma)\) with \(\pi\) PRIMARY and \(\sigma\) SECONDARY, valid for MW (ie. such that \(\langle h_{q-1}\partial_q(\pi), \sigma \rangle\) invertible and \(\langle \partial_{q+1} h_q(\sigma), \pi \rangle\) invertible). It returns a vector of such pairs.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pairs_MW() [2/2]

template<typename CoefficientType , typename ComplexType >

std::vector< PairCell > CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pairs_MW	(	int	q,
		bool &	found,
		size_t	tau
	)		const

Finds all valid PairCell of dimension q for W cointaining tau.

The function searches all pairs of cells \((\pi, \sigma)\) with \(\pi\) PRIMARY and \(\sigma\) SECONDARY (one of them is tau), valid for MW (ie. such that \(\langle h_{q-1}\partial_q(\pi), \sigma \rangle\) invertible and \(\langle \partial_{q+1} h_q(\sigma), \pi \rangle\) invertible). It returns a vector of such pairs.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
[in]	tau	Cell of dimension `q` to pair.

◆ find_pairs_W() [1/2]

template<typename CoefficientType , typename ComplexType >

std::vector< PairCell > CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pairs_W	(	int	q,
		bool &	found
	)		const

Finds all valid PairCell of dimension q for W.

The function searches all pairs of cells \((\sigma, \gamma)\) with \(\sigma\) SECONDARY and \(\gamma\) CRITICAL, valid for W (ie. such that \(\langle g(\gamma), \sigma \rangle\) invertible). It returns a vector of such pairs.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.

◆ find_pairs_W() [2/2]

template<typename CoefficientType , typename ComplexType >

std::vector< PairCell > CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::find_pairs_W	(	int	q,
		bool &	found,
		size_t	tau
	)		const

Finds all valid PairCell of dimension q for W cointaining tau.

The function searches all pairs of cells \((\sigma, \gamma)\) with \(\sigma\) SECONDARY and \(\gamma\) CRITICAL (one of them is tau), valid for W (ie. such that \(\langle g(\gamma), \sigma \rangle\) invertible). It returns the first valid pair found by iterators. It returns a vector of such pairs.

Parameters

[in]	q	Dimension of the pair searched.
[in]	found	Reference to a Boolean variable. The method sets `found` to `true` if a valid pair is found, `false` otherwise.
[in]	tau	Cell of dimension `q` to pair.

◆ get_annotation()

template<typename CoefficientType , typename ComplexType >

HDVF_coreT::CChain CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::get_annotation	(	typename HDVF_coreT::CChain	chain,
		int	dim
	)		const

Gets the annotation of a cycle in the homology basis.

The method returns the image of a cycle by the morphism \(f\), that is, a linear combination of critical cells (corresponding to the decomposition of the cycle in the homology basis). If the annotation has a single non zero coefficient for a given critical cell \(\sigma\), then the cycle belongs to the class of the homology generator \(g(\sigma)\).

Warning: Will raise an error is the chain provided is not a cycle.; The HDVF must be perfect.

Parameters

[in]	chain	The cycle to annotate in the homology basis.
[in]	dim	Dimension of the cycle.

◆ get_coannotation()

template<typename CoefficientType , typename ComplexType >

HDVF_coreT::RChain CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::get_coannotation	(	typename HDVF_coreT::RChain	chain,
		int	dim
	)		const

Gets the co-annotation of a co-cycle in the cohomology basis.

The method returns the image of a co-cycle by the morphism \(g^*\), that is, a linear combination of critical cells (corresponding to the decomposition of the co-cycle in the cohomology basis). If the annotation has a single non zero coefficient for a given critical cell \(\sigma\), then the co-cycle belongs to the class of the cohomology generator \(f^*(\sigma)\).

Warning: Will raise an error is the chain provided is not a co-cycle.; The HDVF must be perfect.

Parameters

[in]	chain	The co-cycle to annotate in the homology basis.
[in]	dim	Dimension of the co-cycle.

◆ M()

template<typename CoefficientType , typename ComplexType >

void CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::M	(	size_t	pi,
		size_t	gamma,
		int	q
	)

M operation.

A pair of cells \((\pi, \gamma)\) of dimension q, with \(\pi\) PRIMARY and \(\gamma\) CRITICAL, is valid for M if \(\langle f(\pi), \gamma \rangle\) is invertible. After the M operation, \(\pi\) becomes CRITICAL and \(\gamma\) become PRIMARY. The M method updates the reduction accordingly (in time \(\mathcal O(n^2)\)).

Parameters

[in]	pi	First cell of the pair (dimension `q`)
[in]	gamma	Second cell of the pair (dimension `q`)
[in]	q	Dimension of the pair

◆ MW()

template<typename CoefficientType , typename ComplexType >

void CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::MW	(	size_t	pi,
		size_t	sigma,
		int	q
	)

MW operation.

A pair of cells \((\pi, \sigma)\) of dimension q, with \(\pi\) PRIMARY and \(\sigma\) SECONDARY, is valid for MW if \(\langle h_{q-1}\partial_q(\pi), \sigma \rangle\) is invertible and \(\langle \partial_{q+1} h_q(\sigma), \pi \rangle\) is invertible. After the MW operation, \(\pi\) becomes SECONDARY and \(\sigma\) become PRIMARY. The MW method updates the reduction accordingly (in time \(\mathcal O(n^2)\)).

Parameters

[in]	pi	First cell of the pair (dimension `q`)
[in]	sigma	Second cell of the pair (dimension `q`)
[in]	q	Dimension of the pair

◆ R()

template<typename CoefficientType , typename ComplexType >

void CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::R	(	size_t	pi,
		size_t	sigma,
		int	q
	)

R operation (cancels a A operation).

A pair of cells \((\pi, \sigma)\) of respective dimension q and q+1, with \(\pi\) PRIMARY and \(\sigma\) SECONDARY, is valid for R if \(\langle h(\pi), \sigma \rangle\) is invertible. After the R operation, \(\pi\) and \(\sigma\) become CRITICAL. The R method updates the reduction accordingly (in time \(\mathcal O(n^2)\)).

Parameters

[in]	pi	First cell of the pair (dimension `q`)
[in]	sigma	Second cell of the pair (dimension `q+1`)
[in]	q	Dimension of the pair

◆ W()

template<typename CoefficientType , typename ComplexType >

void CGAL::HDVF::Hdvf< CoefficientType, ComplexType >::W	(	size_t	sigma,
		size_t	gamma,
		int	q
	)

W operation.

A pair of cells \((\sigma, \gamma)\) of dimension q, with \(\sigma\) SECONDARY and \(\gamma\) CRITICAL, is valid for W if \(\langle g(\gamma), \sigma \rangle\) is invertible. After the W operation, \(\sigma\) becomes CRITICAL and \(\gamma\) become SECONDARY. The W method updates the reduction accordingly (in time \(\mathcal O(n^2)\)).

Parameters

[in]	sigma	First cell of the pair (dimension `q`)
[in]	gamma	Second cell of the pair (dimension `q`)
[in]	q	Dimension of the pair

Inherits from

Definition

Public Types

Public Member Functions

Additional Inherited Members

Constructor & Destructor Documentation

◆ Hdvf()

Member Function Documentation

◆ are_same_cocycles()

◆ are_same_cycles()

◆ find_pair_M() [1/2]

◆ find_pair_M() [2/2]

◆ find_pair_MW() [1/2]

◆ find_pair_MW() [2/2]

◆ find_pair_W() [1/2]

◆ find_pair_W() [2/2]

◆ find_pairs_M() [1/2]

◆ find_pairs_M() [2/2]

◆ find_pairs_MW() [1/2]

◆ find_pairs_MW() [2/2]

◆ find_pairs_W() [1/2]

◆ find_pairs_W() [2/2]

◆ get_annotation()

◆ get_coannotation()

◆ M()

◆ MW()

◆ R()

◆ W()