#include <CGAL/HDVF/Cubical_chain_complex.h>

Definition

template<typename CoefficientType>
class CGAL::HDVF::Cubical_chain_complex< CoefficientType >

The class Cubical_chain_complex represents (topological) chain complexes associated to cubical complexes.

Description

A cubical complex is a set of "square" cells such that: all the faces of a given cell also belong to the complex and any two cells intersect exactly along a common face.

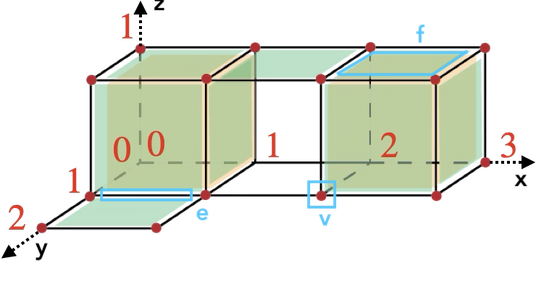
A cell in a cubical complex of dimension q is the cartesian product of \(q\) intervals \([n_1,n_1+\delta_1]\times [n_q,n_q+\delta_q] \) with \(n_i\in \mathbb N \) and \(\delta_i = 0,1\). The dimension of such a cell is \(\sum_{i=1}^q \delta_i\). A 0-cell is thus a vertex, a 1-cell contains one non zero delta (edge along one of the axes), a 2-cell contains two non zero deltas (square along two of the axes), while a 3-cell is a cube...

For instance, \(v = [2,2]\times[1,1]\times[0,0]\), \(e = [0,1]\times[1,1]\times[0,0]\) and \(f = [2,3]\times[0,1]\times[1,1]\).

Given a cubical complex of dimension \(q\) included in \([0,B_1]\times\cdots \times[0,B_q]\), Khalimsky coordinates associate to each cell of the complex a unique coordinate in \([0,2B_1]\times\cdots \times[0,2B_q]\):

\[ \begin{array}{rcl} \sigma & \mapsto & \mathrm{khal}(\sigma) \\ [n_1,n_1+\delta_1]\times\cdots \times [n_q,n_q+\delta_q] & \,\to\, & (2n_1+\delta_1,\ldots,2n_1+\delta_1) \\ \end{array}\]

we set \(N_i = 2B_i+1\) the size of the Khalimsky bounding box along the \(i\)th axis.

The dimension of a cell is the given by the number of odd coordinates. In our previous example, \(B_1=3, B_2=2, B_3=1\), hence \(N_1=7, N_2=5, N_3=3\) and we get the following Khalimsky coordinates: \(\mathrm{khal}(v) = (4,2,0)\), \(\mathrm{khal}(e) = (1,2,0)\) and \(\mathrm{khal}(f) = (5,1,2)\).

The boundary map of the complex is computed by the constructor of the class using the standard formula with Khalimsky coordinates. Given a cell \(\sigma\) with \(\mathrm{khal}(\sigma) = (x_1,\ldots,x_q)\)

\[ \partial(x_1,\ldots,x_q) = \sum_{\substack{i=0\\x_i\text{ odd}}}^q (-1)^{j(i)} \left( (x_1,\ldots,x_i+1,\ldots, x_q) - (x_1,\ldots,x_i-1,\ldots, x_q)\right)\]

where \(j(i)\) is the number of odd coordinates between \(x_1\) and \(x_i\).

Let us also point out that besides Khalimsky coordinates, cells are indexed along each dimension, thus each cell is uniquely determined by its dimension and its index in this dimension (called "base index").

Implementation Details

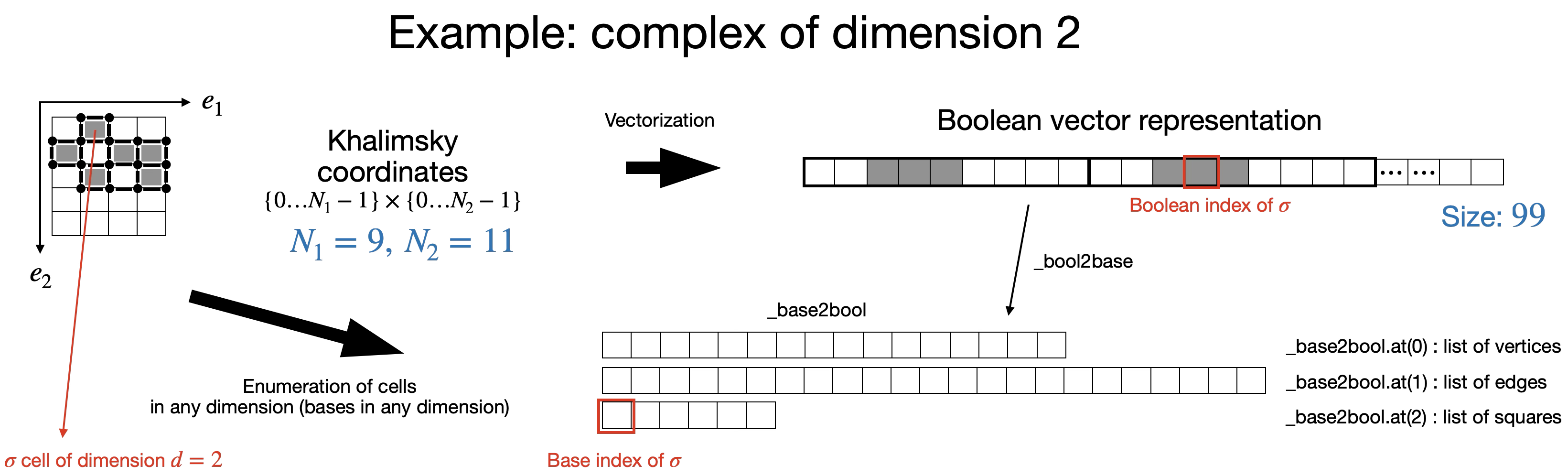
As described above, Khalimsky coordinates provide a convenient tool to identify cells of any dimension. Hence a complex of dimension \(q\) can be encoded by a boolean matrix of size \(N_1\times\cdots\times N_q\) (with previous notations). For convenience, this matrix is vectorized and thus the complex is stored in a boolean vector (denoted by _cells) of size \(N_1\times \cdots \times N_q\).

Cells of any dimension are thus repesented by a given element of this boolean vector and the corresponding index is called their boolean index.

As stated above, besides this boolean representation, topological computations require to identify the bases of cells in any dimension (bases of the free chain groups). Hence, a cell of dimension \(d\) is also identified by its index in the basis of \(d\)-dimensional cells. This index is called its basis index. The vector _bool2base stores, for each dimension, the map between boolean and base indices, while the _base2bool stores, for each dimension, the permutation between base and boolean indices.

Is model of: GeometricChainComplex

Template Parameters

CoefficientType a model of the Ring concept.

Examples: HDVF/example_hdvf_cubical.cpp, HDVF/main_dual_hdvf.cpp, HDVF/main_hdvf.cpp, and HDVF/main_per_hdvf.cpp.

Public Types
enum	typeComplexCube { PRIMAL , DUAL }
	Type used to encode primal or dual construction. More...

typedef std::vector< double >	Point
	Type of vertices coordinates.

typedef OSM::Sparse_chain< CoefficientType, OSM::COLUMN >	CChain
	Type of column-major chains.

typedef OSM::Sparse_chain< CoefficientType, OSM::ROW >	RChain
	Type of row-major chains.

typedef OSM::Sparse_matrix< CoefficientType, OSM::COLUMN >	CMatrix
	Type of column-major sparse matrices.

Public Member Functions
	Cubical_chain_complex ()
	Default constructor (empty cubical complex).

	Cubical_chain_complex (const Cub_object_io &cub, typeComplexCube type)
	Constructor from a Cub_object_io (builds PRIMAL or DUAL associated complex depending on `type`).

Cubical_chain_complex &	operator= (const Cubical_chain_complex &complex)
	Assignment operator for cubical chain complexes.

CChain	d (size_t id_cell, int q) const
	Returns the boundary of the cell id_cell in dimension q.

RChain	cod (size_t id_cell, int q) const
	Returns the co-boundary of the cell id_cell in dimension q.

int	dim () const
	Returns the dimension of the complex.

size_t	nb_cells (int q) const
	Returns the number of cells in a given dimension.

const vector< CMatrix > &	get_bnd_matrices () const
	Returns a constant reference to the vector of boundary matrices (along each dimension).

const CMatrix &	get_bnd_matrix (int q) const
	Returns a copy of the dim-th boundary matrix (ie.

std::vector< size_t >	bottom_faces (size_t id_cell, int q) const
	Returns dimension 0 cells indexes included in the cell with index id_cell of dimension q.

template<typename CoefficientT , int ChainTypeF>
CChain	cofaces_chain (OSM::Sparse_chain< CoefficientT, ChainTypeF > chain, int q) const
	Returns the cofaces of a given chain in dimension `q`.

void	print_complex () const
	Prints informations on the complex.

size_t	get_id () const
	Gets (unique) object Id.

Point	get_vertex_coords (size_t i) const
	Gets the coordinates of the ith vertex.

const std::vector< Point > &	get_vertices_coords () const
	Gets the vector of vertices coordinates

Static Public Member Functions
template<typename LabelType = int>
static void	chain_complex_to_vtk (const Cubical_chain_complex< CoefficientType > &K, const std::string &filename, const std::vector< std::vector< LabelType > > *labels=NULL, string label_type_name="int")
	END Methods of the Cubical_chain_complex concept.

static void	chain_complex_chain_to_vtk (const Cubical_chain_complex< CoefficientType > &K, const std::string &filename, const OSM::Sparse_chain< CoefficientType, OSM::COLUMN > &chain, int q, size_t cellId=-1)
	Exports a chain over a cubical complex to a VTK file.

Public Attributes
friend	Duality_cubical_complex_tools< CoefficientType >
	Friend class `Duality_cubical_complex_tools` provides tools for Alexander duality.

Protected Member Functions
std::vector< size_t >	get_size_bb () const

std::vector< size_t >	get_P () const

std::vector< bool >	get_cells () const

std::vector< std::vector< size_t > >	get_base2bool () const

std::vector< std::map< size_t, size_t > >	get_bool2base () const

CChain	boundary_cell (size_t index_base, int dim) const

bool	is_valid_cell (const std::vector< size_t > &cell) const

bool	is_valid_cell (size_t id_cell) const

vector< size_t >	khal_to_verts (vector< size_t > c) const

void	initialize_cells (const Cub_object_io &cub, typeComplexCube type)

std::vector< size_t >	ind2khal (size_t index) const
	Computes Khalimsky coordinates from boolean index.

size_t	khal2ind (const std::vector< size_t > &base_indices) const

std::vector< size_t >	ind2vox (size_t index, vector< size_t > B, size_t max_size) const

size_t	vox2ind (const std::vector< size_t > &base_indices, vector< size_t > B, size_t max_size) const

void	calculate_d (int q)

void	insert_cell (size_t cell)

int	calculate_dimension (const std::vector< size_t > &cell) const

int	calculate_dimension (size_t cell_index) const

std::vector< size_t >	calculate_boundaries (size_t cell) const

Protected Attributes
int	_dim

std::vector< size_t >	_size_bb

std::vector< size_t >	_P

std::vector< bool >	_cells

std::vector< std::vector< size_t > >	_base2bool

std::vector< std::map< size_t, size_t > >	_bool2base

std::vector< CMatrix >	_d

Member Enumeration Documentation

◆ typeComplexCube

template<typename CoefficientType >

enum CGAL::HDVF::Cubical_chain_complex::typeComplexCube

Type used to encode primal or dual construction.

Enumerator
PRIMAL
DUAL

Constructor & Destructor Documentation

◆ Cubical_chain_complex() [1/2]

template<typename CoefficientType >

CGAL::HDVF::Cubical_chain_complex< CoefficientType >::Cubical_chain_complex ( )

Default constructor (empty cubical complex).

Builds an empty cubical complex.

◆ Cubical_chain_complex() [2/2]

template<typename CoefficientType >

CGAL::HDVF::Cubical_chain_complex< CoefficientType >::Cubical_chain_complex	(	const Cub_object_io &	cub,
		typeComplexCube	type
	)

Constructor from a Cub_object_io (builds PRIMAL or DUAL associated complex depending on type).

Builds the cubical complex associated to a a set of cells (vertices, edges, squares, cubes...), ie. performs the down closure of cells and set the boundary matrices in any dimension. Given a set of cells:

if the type is PRIMAL, the constructor builds the associated complex as such (see below middle), which comes to encode \(3^q-1\) connectivity (with \(q\) the dimension of the complex)
if the type is DUAL and the Cub_object_io contains only cells of maximal dimension (ie. binary object), the constructor build the dual associated complex (see below right), which comes to encode \(2q\) connectivity (with \(q\) the dimension of the complex)

Parameters

[in]	cub	A Cub_object_io containing a set of "cubical" cells.
[in]	type	Type of construction used (PRIMAL or DUAL).

Member Function Documentation

◆ bottom_faces()

template<typename CoefficientType >

std::vector< size_t > CGAL::HDVF::Cubical_chain_complex< CoefficientType >::bottom_faces	(	size_t	id_cell,
		int	q
	)		const

Returns dimension 0 cells indexes included in the cell with index id_cell of dimension q.

Returns the dimension 0 vertices indexes included in the cell with index id_cell of dimension q.

Parameters

[in]	id_cell	Index of the cell.
[in]	q	Dimension of the cell.

Returns: A vector of 0-cells indices.

◆ chain_complex_chain_to_vtk()

template<typename CoefficientType >

void CGAL::HDVF::Cubical_chain_complex< CoefficientType >::chain_complex_chain_to_vtk	(	const Cubical_chain_complex< CoefficientType > &	K,
		const std::string &	filename,
		const OSM::Sparse_chain< CoefficientType, OSM::COLUMN > &	chain,
		int	q,
		size_t	cellId = `-1`
	)

static

Exports a chain over a cubical complex to a VTK file.

The method generates legacy text VTK files. All the cells of the chain with non zero coefficient are exported. If a cellId is provided, labels are exported in a VTK property (2 for all cells, 0 for cell of index cellId). The index of each cell is exported in a CellID property.

Parameters

[in]	K	Cubical complex exported.
[in]	filename	Output file root (output filenames will be built from this root).
[in]	chain	Sparse_chain exported (all the cells with non-zero coefficients in the chain are exported to vtk).
[in]	q	Dimension of the cells of the chain.
[in]	cellId	If different from MAX_SIZE_T, labels are exported to distinguish cells of the chain (label 2) from cellId cell (label 0).

◆ chain_complex_to_vtk()

template<typename CoefficientType >

template<typename LabelType = int>

static void CGAL::HDVF::Cubical_chain_complex< CoefficientType >::chain_complex_to_vtk	(	const Cubical_chain_complex< CoefficientType > &	K,
		const std::string &	filename,
		const std::vector< std::vector< LabelType > > *	labels = `NULL`,
		string	label_type_name = `"int"`
	)

static

END Methods of the Cubical_chain_complex concept.

Exports a cubical complex (plus, optionally, labels) to a VTK file.

The method generates legacy text VTK files. Labels are exported as such in a VTK property, together with CellID property, containing the index of each cell.

Template Parameters

LabelType Type of labels provided (default: int).

Parameters

[in]	K	Cubical complex exported.
[in]	filename	Output file root (output filenames will be built from this root).
[in]	labels	Pointer to a vector of labels in each dimension. (*labels).at(q) is the set of integer labels of cells of dimension q. If labels is NULL, only CellID property is exported.
[in]	label_type_name	Typename used in vtk export (e.g. "int" or "unsigned_long", see VTK manual ).

◆ cod()

template<typename CoefficientType >

RChain CGAL::HDVF::Cubical_chain_complex< CoefficientType >::cod	(	size_t	id_cell,
		int	q
	)		const

Returns the co-boundary of the cell id_cell in dimension q.

Returns a row-major chain containing the co-boundary of the cell id_cell in dimension q (so actually a row of the boundary matrix).

Warning: As the boundary matrix is stored column-major, this entails crossing the full matrix to extract the row coefficients (O(number of non empty columns))

Parameters

[in]	id_cell	Index of the cell.
[in]	q	Dimension of the cell.

Returns: The row-major chain containing the co-boundary of the cell id_cell in dimension q.

◆ cofaces_chain()

template<typename CoefficientType >

template<typename CoefficientT , int ChainTypeF>

CChain CGAL::HDVF::Cubical_chain_complex< CoefficientType >::cofaces_chain	(	OSM::Sparse_chain< CoefficientT, ChainTypeF >	chain,
		int	q
	)		const

Returns the cofaces of a given chain in dimension q.

The resulting chain lies in dimension q+1 and is null if this dimension exceeds the dimension of the complex.

◆ d()

template<typename CoefficientType >

CChain CGAL::HDVF::Cubical_chain_complex< CoefficientType >::d	(	size_t	id_cell,
		int	q
	)		const

Returns the boundary of the cell id_cell in dimension q.

Returns a copy of the column-major chain stored in the boundary matrix of dimension q: boundary of the cell id_cell in dimension q.

Parameters

[in]	id_cell	Index of the cell.
[in]	q	Dimension of the cell.

Returns: The column-major chain containing the boundary of the cell id_cell in dimension q.

◆ dim()

template<typename CoefficientType >

int CGAL::HDVF::Cubical_chain_complex< CoefficientType >::dim ( ) const

Returns the dimension of the complex.

Returns the dimension of the cubical complex.

Returns: The dimension of the complex..

◆ get_bnd_matrices()

template<typename CoefficientType >

const vector< CMatrix > & CGAL::HDVF::Cubical_chain_complex< CoefficientType >::get_bnd_matrices ( ) const

Returns a constant reference to the vector of boundary matrices (along each dimension).

Returns a constant reference to the vector of boundary matrices along each dimension. The q-th element of this vector is a column-major sparse matrix containing the boundaries of q-cells (ie. rows encode q-1 cells and columns q cells).

Returns: Returns a constant reference to the vector of column-major boundary matrices along each dimension.

◆ get_bnd_matrix()

template<typename CoefficientType >

const CMatrix & CGAL::HDVF::Cubical_chain_complex< CoefficientType >::get_bnd_matrix ( int q ) const

Returns a copy of the dim-th boundary matrix (ie.

column-major matrix of \(\partial_q\)).

It is a column-major sparse matrix containing the boundaries of dim-cells (ie. rows encode q-1 cells and columns q cells).

Parameters

[in] q Dimension of the boundary matrix (ie. columns will contain the boundary of dimension q cells).

Returns: A column-major sparse matrix containing the matrix of the boundary operator of dimension q.

◆ get_id()

template<typename CoefficientType >

size_t CGAL::HDVF::Cubical_chain_complex< CoefficientType >::get_id ( ) const

Gets (unique) object Id.

For comparison of constant references to the complex.

◆ nb_cells()

template<typename CoefficientType >

size_t CGAL::HDVF::Cubical_chain_complex< CoefficientType >::nb_cells ( int q ) const

Returns the number of cells in a given dimension.

Parameters

[in] q Dimension along which the number of cells is returned.

Returns: Number of cells in dimension q.

◆ operator=()

template<typename CoefficientType >

Cubical_chain_complex & CGAL::HDVF::Cubical_chain_complex< CoefficientType >::operator= ( const Cubical_chain_complex< CoefficientType > & complex )

Assignment operator for cubical chain complexes.

Stores a copy of an cubical chain complex in *this.

Parameters

[in] complex The cubical chain complex which will be copied.

◆ print_complex()

template<typename CoefficientType >

void CGAL::HDVF::Cubical_chain_complex< CoefficientType >::print_complex ( ) const

Prints informations on the complex.

Displays the number of cells in each dimension and the boundary matrix in each dimension.

Definition

Description

Implementation Details

Public Types

Public Member Functions

Static Public Member Functions

Public Attributes

Protected Member Functions

Protected Attributes

Member Enumeration Documentation

◆ typeComplexCube

Constructor & Destructor Documentation

◆ Cubical_chain_complex() [1/2]

◆ Cubical_chain_complex() [2/2]

Member Function Documentation

◆ bottom_faces()

◆ chain_complex_chain_to_vtk()

◆ chain_complex_to_vtk()

◆ cod()

◆ cofaces_chain()

◆ d()

◆ dim()

◆ get_bnd_matrices()

◆ get_bnd_matrix()

◆ get_id()

◆ nb_cells()

◆ operator=()

◆ print_complex()