#include <CGAL/HDVF/Abstract_simplicial_chain_complex.h>

Inherited by CGAL::HDVF::Simplicial_chain_complex< CoefficientType >.

Definition

template<typename CoefficientType>
class CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >

The class Abstract_simplicial_chain_complex represents (topological) chain complexes associated to abstract simplicial complexes.

An abstract simplicial complex is a set of simplices, also called cells (class Simplex) such that: all the faces of a given simplex also belong to the complex and any two simplices intersect exactly along a common face.

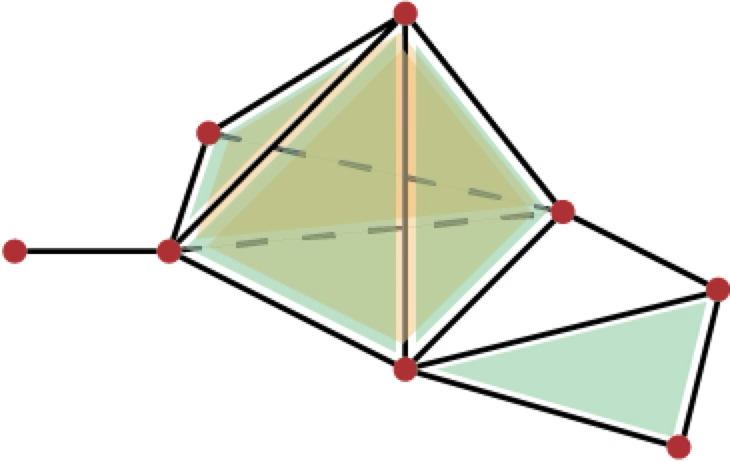
A simplex of dimension q contains exactly q+1 vertices (we will thus denote it by \(\langle v_0, \ldots, v_q \rangle\)). A 0-cell is thus a vertex, a 1-cell contains two vertices (edge), a 2-cell contains three vertices (triangle) while a 3-cell is a tetrahedron.

The boundary map of the complex is computed by the constructor of the class using the standard formula:

\[ \partial_q\left( \langle v_0, \ldots, v_q \rangle\right) = \sum_{i=0}^q (-1)^i\cdot \langle v_0, \ldots, \widehat{v_i}, \cdots, v_q \rangle\]

where \(\langle v_0, \ldots, \widehat{v_i}, \cdots, v_q \rangle\) denotes the \(q-1\)-simplex with \(v_i\) omitted. Hence, matrices of boundary maps are stored in each dimension using sparse matrices (in column-major mode).

Let us also point out that cells are indexed along each dimension, thus each simplex is uniquely determined by its dimension and its index in this dimension.

Is model of: AbstractChainComplex

Template Parameters

CoefficientType a model of the Ring concept.

Examples: HDVF/main_hdvf.cpp.

Public Types
typedef OSM::Sparse_chain< CoefficientType, OSM::COLUMN >	CChain
	Type of column-major chains.

typedef OSM::Sparse_chain< CoefficientType, OSM::ROW >	RChain
	Type of row-major chains.

typedef OSM::Sparse_matrix< CoefficientType, OSM::COLUMN >	CMatrix
	Type of column-major sparse matrices.

Public Member Functions
	Abstract_simplicial_chain_complex (int q=0)
	Default constructor (empty simplicial complex of dimension `q`).

	Abstract_simplicial_chain_complex (const Mesh_object_io &mesh)
	Constructor from a `Mesh_object_io`.

Abstract_simplicial_chain_complex &	operator= (const Abstract_simplicial_chain_complex &complex)
	Assignment operator for abstract simplicial chain complexes.

CChain	d (size_t id_cell, int q) const
	Returns the boundary of the cell id_cell in dimension q.

RChain	cod (size_t id_cell, int q) const
	Returns the co-boundary of the cell id_cell in dimension q.

int	dim () const
	Returns the dimension of the complex.

size_t	nb_cells (int q) const
	Returns the number of cells in a given dimension.

const vector< CMatrix > &	get_bnd_matrices () const
	Returns a constant reference to the vector of boundary matrices (along each dimension).

const CMatrix &	get_bnd_matrix (int q) const
	Returns a copy of the dim-th boundary matrix (i.e. column-major matrix of \(\partial_q\)).

std::vector< size_t >	bottom_faces (size_t id_cell, int q) const
	Returns dimension 0 simplices indexes included in the cell with index id_cell of dimension q.

template<typename CoefficientT , int ChainTypeF>
CChain	cofaces_chain (OSM::Sparse_chain< CoefficientT, ChainTypeF > chain, int q) const
	Returns the cofaces of a given chain in dimension `q`.

std::ostream &	print_complex (std::ostream &out=std::cout) const
	Prints informations on the complex.

size_t	get_id () const
	Get (unique) object Id.

Protected Member Functions
void	calculate_d (int q) const

void	insert_simplex (const Simplex &tau)

Protected Attributes
int	_dim

std::vector< std::vector< Simplex > >	_ind2simp

std::vector< std::map< Simplex, size_t > >	_simp2ind

std::vector< size_t >	_nb_cells

std::vector< CMatrix >	_d

Constructor & Destructor Documentation

◆ Abstract_simplicial_chain_complex() [1/2]

template<typename CoefficientType >

CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::Abstract_simplicial_chain_complex ( int q = 0 )

Default constructor (empty simplicial complex of dimension q).

Builds an empty abstract simplicial complex of dimension q.

◆ Abstract_simplicial_chain_complex() [2/2]

template<typename CoefficientType >

CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::Abstract_simplicial_chain_complex ( const Mesh_object_io & mesh )

Constructor from a Mesh_object_io.

Builds the abstract simplicial complex associated to a triangular mesh (i.e. performs the down closure of cells and set the boundary matrices in any dimension).

Parameters

[in] mesh A Mesh_object_io containing a triangular mesh.

Member Function Documentation

◆ bottom_faces()

template<typename CoefficientType >

std::vector< size_t > CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::bottom_faces	(	size_t	id_cell,
		int	q
	)		const

Returns dimension 0 simplices indexes included in the cell with index id_cell of dimension q.

Returns the dimension 0 simplices indexes included in the cell with index id_cell of dimension q.

Warning: This does not come to return vertices indices, as dimension 0 simplices enumerate vertices in any order. For instance, if an abstract simplicial complex is built from 3 vertices {1,2,3} such that the enumeration of dimension 0 simplices is: id0: 3, id1 : 2, id2: 1 then the bottom_faces of the 1-simplex {1,2} are two 0-simplices with id 2 and 1.

Parameters

[in]	id_cell	Index of the cell.
[in]	q	Dimension of the cell.

Returns: A vector of 0-simplices indexes.

◆ cod()

template<typename CoefficientType >

RChain CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::cod	(	size_t	id_cell,
		int	q
	)		const

Returns the co-boundary of the cell id_cell in dimension q.

Returns a row-major chain containing the co-boundary of the cell id_cell in dimension q (so actually a row of the boundary matrix).

Warning: As the boundary matrix is stored column-major, this entails crossing the full matrix to extract the row coefficients (O(number of non empty columns))

Parameters

[in]	id_cell	Index of the cell.
[in]	q	Dimension of the cell.

Returns: The row-major chain containing the co-boundary of the cell id_cell in dimension q.

◆ cofaces_chain()

template<typename CoefficientType >

template<typename CoefficientT , int ChainTypeF>

CChain CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::cofaces_chain	(	OSM::Sparse_chain< CoefficientT, ChainTypeF >	chain,
		int	q
	)		const

Returns the cofaces of a given chain in dimension q.

The resulting chain lies in dimension q+1 and is null if this dimension exceeds the dimension of the complex.

◆ d()

template<typename CoefficientType >

CChain CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::d	(	size_t	id_cell,
		int	q
	)		const

Returns the boundary of the cell id_cell in dimension q.

Returns a copy of the column-major chain stored in the boundary matrix of dimension dim: boundary of the cell id_cell in dimension q.

Parameters

[in]	id_cell	Index of the cell.
[in]	q	Dimension of the cell.

Returns: The column-major chain containing the boundary of the cell id_cell in dimension q.

◆ dim()

template<typename CoefficientType >

int CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::dim ( ) const

Returns the dimension of the complex.

Returns the dimension of the simplicial complex (i.e. largest dimension of cells).

Returns: The dimension of the complex..

◆ get_bnd_matrices()

template<typename CoefficientType >

const vector< CMatrix > & CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::get_bnd_matrices ( ) const

Returns a constant reference to the vector of boundary matrices (along each dimension).

Returns a constant reference to the vector of boundary matrices along each dimension. The q-th element of this vector is a column-major sparse matrix containing the boundaries of q-cells (i.e. rows encode q-1 cells and columns q cells).

Returns: Returns a constant reference to the vector of column-major boundary matrices along each dimension.

◆ get_bnd_matrix()

template<typename CoefficientType >

const CMatrix & CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::get_bnd_matrix ( int q ) const

Returns a copy of the dim-th boundary matrix (i.e. column-major matrix of \(\partial_q\)).

It is a column-major sparse matrix containing the boundaries of q-cells (i.e. rows encode q-1 cells and columns q cells).

Parameters

[in] q Dimension of the boundary matrix (i.e. columns will contain the boundary of dimension q cells).

Returns: A column-major sparse matrix containing the matrix of the boundary operator of dimension q.

◆ get_id()

template<typename CoefficientType >

size_t CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::get_id ( ) const

Get (unique) object Id.

For comparison of constant references to the complex.

◆ nb_cells()

template<typename CoefficientType >

size_t CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::nb_cells ( int q ) const

Returns the number of cells in a given dimension.

Parameters

[in] q Dimension along which the number of cells is returned.

Returns: Number of cells in dimension q.

◆ operator=()

template<typename CoefficientType >

Abstract_simplicial_chain_complex & CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::operator= ( const Abstract_simplicial_chain_complex< CoefficientType > & complex )

Assignment operator for abstract simplicial chain complexes.

Stores a copy of an abstract simplicial chain complex in *this.

Parameters

[in] complex The abstract simplicial chain complex which will be copied.

◆ print_complex()

template<typename CoefficientType >

std::ostream & CGAL::HDVF::Abstract_simplicial_chain_complex< CoefficientType >::print_complex ( std::ostream & out = std::cout ) const

Prints informations on the complex.

Displays the number of cells in each dimension and the boundary matrix in each dimension.

Definition

Public Types

Public Member Functions

Protected Member Functions

Protected Attributes

Constructor & Destructor Documentation

◆ Abstract_simplicial_chain_complex() [1/2]

◆ Abstract_simplicial_chain_complex() [2/2]

Member Function Documentation

◆ bottom_faces()

◆ cod()

◆ cofaces_chain()

◆ d()

◆ dim()

◆ get_bnd_matrices()

◆ get_bnd_matrix()

◆ get_id()

◆ nb_cells()

◆ operator=()

◆ print_complex()