|
CGAL 6.2 - 3D Generalized Barycentric Coordinates
|
|
CGAL 6.2 - 3D Generalized Barycentric Coordinates
|
Barycentric coordinates are an important tool in computer graphics and geometric modeling. Originally, these coordinates were used to represent a given point with respect to a simplex but have been later generalized to more complex shapes.
The package 3D Generalized Barycentric Coordinates offers an efficient and robust implementation of three-dimensional closed-form, generalized barycentric coordinates defined for convex simplicial polytopes.
In particular, this package includes an implementation of Wachspress, discrete harmonic, mean value, and one extra function to calculate barycentric coordinates with respect to tetrahedra. In this implementation, we restrict our polyhedra to convex ones with triangular faces, although some of the coordinates may accept non-convex polyhedra. The calculated coordinates are not normalized.
Wachspress, discrete harmonic, and mean value coordinates are all generalized barycentric coordinates that can be computed analytically. Each of the three analytic coordinates can be computed either by a free function or a function object (Functor). Tetrahedron coordinates can be computed only through the free function.
Similarly to Barycentric_coordinates::Computation_policy_2 in the 2D package, we can specify a computation policy Barycentric_coordinates::Computation_policy_3, which can be FAST or FAST_WITH_EDGE_CASES for each of the three analytical coordinates. The difference between them is that FAST_WITH_EDGE_CASES treats points near the boundaries by projecting them onto the face of the polyhedron and then calculating triangle coordinates. Note that, unlike the 2D package, no implementation of a PRECISE algorithm is yet available.
The output of each method are the coordinates for a point with respect to each vertex of the mesh. The number of coordinates being the same as the number of vertices, and the ordering is also the same.
All class and function templates are parameterized by a traits class, which is a model of the concept BarycentricTraits_3. It provides all necessary geometric primitives, predicates, and constructions, which are required for the computation. All models of Kernel can be used. A polyhedron is provided as a model of the concept FaceListGraph with a property map that maps a vertex from the polyhedron to BarycentricTraits_3::Point_3.
To facilitate the process of learning this package, we provide various examples with basic usage of different barycentric components.
In this example, we use the global function tetrahedron_coordinates(). We compute coordinates for the tetrahedron defined by the points (0,0,0), (1,0,0), (0,1,0), and (0,0,1). We use points inside, outside and at the boundary of the tetrahedron.
File Barycentric_coordinates_3/tetrahedron_coordinates.cpp
In this example, we generate 250 random points inside a unit sphere, centered at the origin. Then we take the convex hull of this set of points and use this as our polyhedron. Finally, we calculate Wachspress coordinates for each of these 250 points.
File Barycentric_coordinates_3/wachspress_coordinates_3.cpp
This example is very similar to the one used with tetrahedron coordinates. We start with a regular icosahedron and for points inside, outside and on the boundary, we calculate discrete harmonic coordinates. In this example, we use the fast with edge cases algorithm because it properly handles points very close to the boundaries.
File Barycentric_coordinates_3/discrete_harmonic_coordinates_3.cpp
This example shows how to compute mean value coordinates for a set of points in a star-shaped polyhedron. We note that this type of coordinate is well-defined for a concave polyhedron but it may yield negative coordinate values for points outside the polyhedron's kernel (shown in blue).
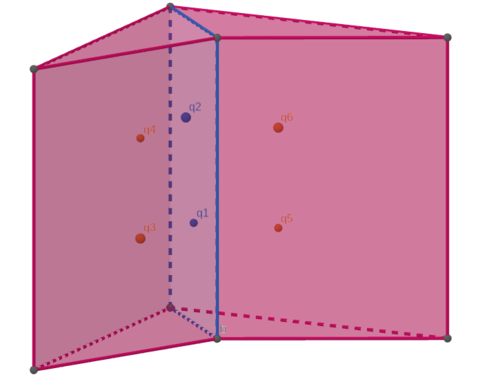
Figure 109.1 The star-shaped polyhedron used in mean_value_coordinates_3.cpp and the six query points, for which the mean value barycentric coordinates are computed.
File Barycentric_coordinates_3/mean_value_coordinates_3.cpp
This example shows how to deform a simple smooth sphere into another topologically equivalent shape. To achieve this, we create a box that encloses the sphere; then we calculate the barycentric coordinates of each vertex with respect to the box. After deforming the box, we use the barycentric coordinates to relocate the vertices of the sphere.
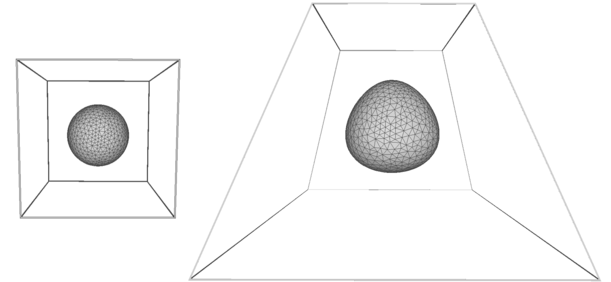
Figure 109.2 The shape on the left is deformed into the shape on the right.
File Barycentric_coordinates_3/shape_deformation_3.cpp
The precision of each coordinate depends on the used Kernel. If an inexact kernel is used and the user is not sure whether the points are located near the boundaries, FAST_WITH_EDGE_CASES algorithm should be used. Implementation details are described in [1] for Wachspress and mean value coordinates, and in [2] for discrete harmonic coordinates.
For each coordinate, it is necessary to make divisions by the signed distance between the query point and each face. So, if one of these distances is zero or close to zero (query point on the boundary), it will cause a division by zero error or numerical instability, respectively. To this end we introduce the FAST_WITH_EDGE_CASES algorithm. Its main purpose is to extend the region where the analytical coordinates are well-defined. It adds the guarantee to calculate points near the boundaries. The way it works is simple: before calculating any coordinate, the algorithm checks, for each face, if the distance between the query point and the supporting plane of the face is less than a predetermined tolerance. If so, instead of calculating the analytical form of the coordinates, it decomposes the query point with respect to this particular face and then calculates triangle coordinates. However, for Wachspress coordinates, the 2D version is used because the faces are not necessarily triangular. Note that for every vertex that does not belong to this face, the coordinate value will be zero.
We adopt the simple formula below to compute tetrahedron coordinates of the query point q:
where \(V_i\) is the signed volume of the sub-tetrahedron opposite to the vertex \(i\), i.e., the tetrahedron where the vertex \(i\) is replaced by the query point q. \(V\) is the total volume of the tetrahedron, that is \(V = V_0 + V_1 + V_2 + V_3\).
These coordinates can be computed exactly if an exact number type is chosen, for any query point and with respect to any non-degenerate tetrahedron. No special cases are handled. The computation always yields the correct result. The notion of correctness depends on the precision of the used number type. Note that for exterior points some coordinate values will be negative.
For each vertex \(v\), let \(f_0, f_1, ..., f_{k-1}\) be the \(k\) faces incident to \(v\). We are assuming that the faces are taken in counterclockwise order.
We can define \({p_f}({q}) = \frac{{n_f}}{h_f({q})}\), and \(h_f({q}) = ({v} - {q})\cdot {n_f}\) as the perpendicular distance of \(q\) to \(f\). For the face \(f\), let \({n_f}\) denote its unit outward normal.
The following formula is adopted to compute Wachspress coordinates of the query point q:
In this implementation, Wachspress coordinates are well defined in the closure of any convex polyhedra. If an exact number type is chosen, they are computed in an exact manner.
We adopt the formula below to compute discrete harmonic coordinates of the query point q:
where, within a triangle face \(T = \{v0, v1, v2\}\), \(\theta_i^T\) is the dihedral angle between \(T\) and triangle \(\{x,v_{i+1}\), \(v_{i−1}\}\), and \(h_i^T\) is the edge length \(|v_{i+1} − v_{i−1}|\).
Discrete harmonic coordinates cannot be computed exactly due to a square root operation. Although, if an exact number type is used, the default precision of the computation depends only on two CGAL functions: CGAL::to_double() and CGAL::sqrt(). In this implementation, discrete harmonic coordinates are well defined in the closure of any convex polyhedra with triangular faces. Unlike Wachspress coordinates, they are not necessarily positive.
The following formula is adopted to compute mean value coordinates of the query point q:
where a vertex v is projected onto the point (unit vector) \(e_v = \frac{({v} - {q})}{|{v - q}|}\), and \({m_i} = \frac{{e_i} \times {e_{i+1}}}{|{e_i} \times {e_{i+1}}|}\). \(\beta_j \in (0, \pi)\) is the angle between \(e_i\) and \(e_{i+1}\).
Like discrete harmonic, mean value coordinates cannot be exactly computed due to a square root operation. In this implementation, mean value coordinates are well defined everywhere in the space, but just for polyhedra with triangular faces. Also, they are non-negative in the kernel of a star-shaped polyhedron.
Efficiency is crucial in this implementation. These coordinates are used in applications that require calculations for millions of points; thus, developing metrics to evaluate performance is necessary. In this section, we present benchmark results for each algorithm.
The benchmark and runtimes are evaluated by regularly sampling \(n^3\) ( \(n\) varying from 1 to 100) points from the interior of the unit cube, and calculating their coordinate values (see figure below).
The results are averaged over 10 executions and represented in a log-log scale plot.
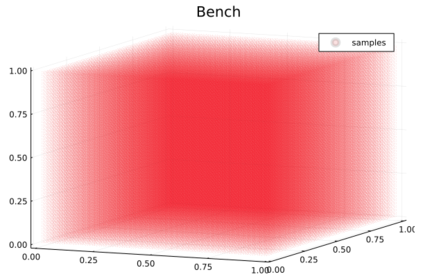
Figure 109.3 The points shown in red are the sample points used to make the benchmark.
The performance strongly depends on the chosen kernel, for this test, we choose to use Simple_cartesian<double> because is much faster than others. Also, we can see that time (WP) << time (DH) < time (MV). This happens because the Wachspress implementation has fewer instructions per loop than the other two. For 100k points those generalized barycentric coordinates are calculated within a convex hull with 500 vertices the timings are 17.5s (WP), 25.4s (DH) and 33.3s (MV).
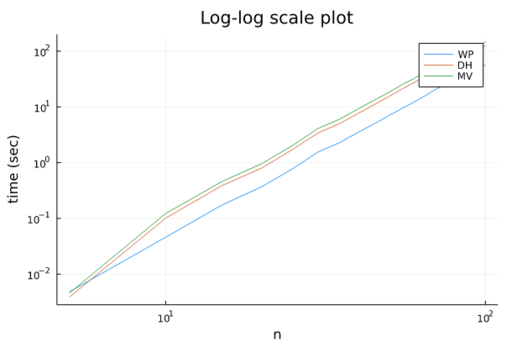
Figure 109.4 Time in seconds to compute \(n^3\) coordinate values for a cube. Wachspress (blue), discrete harmonic (orange), and mean value (green).
Tetrahedron coordinates are not shown in the same plot because the test is slightly different. For this one, we simply show in the table below the results for some pre-defined quantity of points. The test is done by regularly sampling strictly interior points with respect to a tetrahedron with unit sides that lie on the coordinate axis.
| Number of points | Total time (in seconds) |
|---|---|
| 50000 | 0.09 |
| 100000 | 0.19 |
| 500000 | 0.82 |
| 1000000 | 1.67 |
| 5000000 | 8.36 |
To benchmark each coordinate, we used a 2.5 GHz Intel Core i7 processor (8 cores) and 32 GB DDR4 2933MHz memory. The installed operating system was Windows 11.
This package was introduced during GSoC 2021 and implemented by Antonio Gomes under the supervision of Dmitry Anisimov. Sven Oesau finished the final work on API and documentation.