|
CGAL 6.2 - Boolean Operations on Meshes
|
|
CGAL 6.2 - Boolean Operations on Meshes
|
The computation of mesh Boolean operations is one of the most essential parts of the geometry processing toolkit, with numerous applications in CAD and computer graphics. As an example, it constitutes the essential operation of Constructive Solid Geometry (CSG).
This CGAL package offers functions to compute the union, intersection, and difference of volumes bounded by triangle meshes. The core of the method is the corefinement technique, which refines two meshes such that they become conformal. This technique is re-used to also propose functions that enable trimming a mesh ("clipping") and bisecting a mesh ("splitting") with a plane, a box, or another mesh.
We begin by introducing the core concepts of this package in Definitions. Mesh Boolean functions and their input requirements are described in Computing Mesh Boolean Operations, and the guarantees on the output are discussed in Kernel Choice and Output Validity. Related functions for clipping, splitting, and slicing are documented in Clipping and Splitting Meshes and Slicer.
Corefinement: Given two triangulated surface meshes, the corefinement of these two meshes consists in refining both meshes such that their intersection polylines form a subset of the edges of both refined meshes.
Autorefinement: Given a triangle mesh or a triangle soup, the autorefinement consists in refining the mesh/soup such that all intersections between triangles form a subset of the edges of the output.
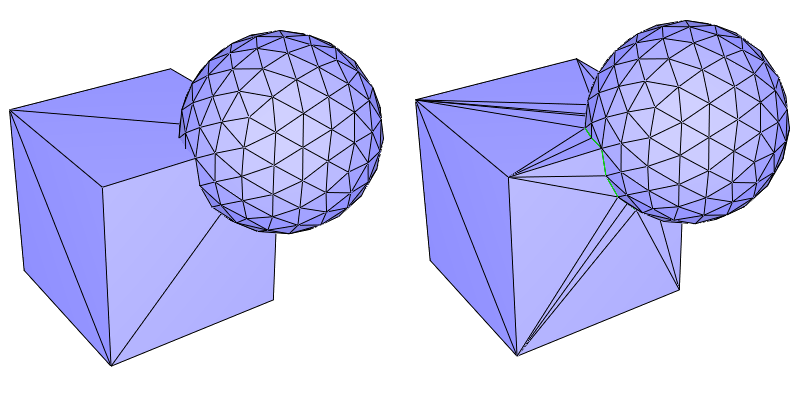
Figure 76.2 Corefinement of two triangulated surface meshes. (Left) Input meshes; (Right) The two input meshes after corefinement. The common edges of the two meshes are drawn in green.
Volume bounded by a triangulated surface mesh Given a closed triangulated surface mesh, each connected component splits the 3D space into two subspaces. The vertex sequence of each face of a component is seen either clockwise or counterclockwise from these two subspaces. The subspace that sees the sequence in a clockwise (resp. counterclockwise) manner is on the negative (resp. positive) side of the component. Given a closed triangulated surface mesh tm with no self-intersections, the connected components of tm divide the 3D space into subspaces. We say that tm bounds a volume if each subspace lies exclusively on the positive (or negative) side of all the incident connected components of tm. The volume bounded by tm is the union of all subspaces that are on negative sides of their incident connected components of tm.
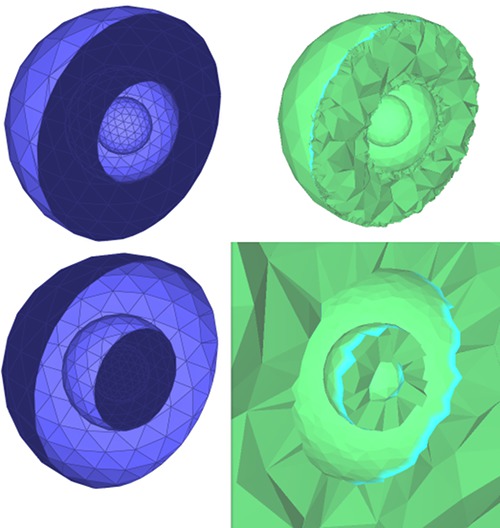
Figure 76.3 Volumes bounded by a triangulated surface mesh: The figure shows meshes representing three nested spheres (three connected components). The left side of the picture shows a clipped triangulated surface mesh, with the two possible orientations of the faces for which a volume is bounded by the mesh. The positive and negative sides of each connected component are displayed in light and dark blue, respectively. The right part of the picture shows clipped tetrahedral meshes of the corresponding bounded volumes.
Corefinement of two triangulated surface meshes can be performed using the function CGAL::Polygon_mesh_processing::corefine(). If constrained edge maps are provided, edges belonging to the intersection of the input meshes will be marked as constrained. Additionally, if a constrained edge is split during corefinement, the resulting sub-edges will also be marked as constrained.
Example: PMP_Boolean_operations/corefinement_SM.cpp
The function CGAL::Polygon_mesh_processing::autorefine_triangle_soup() provides a way to refine a triangle soup using the intersections of the triangles from the soup. In particular, if some points are duplicated they will be merged.
Example: PMP_Boolean_operations/soup_autorefinement.cpp
Corefinement of two triangulated surface meshes is a natural basis for computing Boolean operations on volumes. Given two triangulated surface meshes, each bounding a volume, the following functions are provided:
CGAL::Polygon_mesh_processing::corefine_and_compute_union(),CGAL::Polygon_mesh_processing::corefine_and_compute_intersection(),CGAL::Polygon_mesh_processing::corefine_and_compute_difference().respectively compute the union, intersection, and difference of the two volumes.
If several Boolean operations must be computed at the same time, the function CGAL::Polygon_mesh_processing::corefine_and_compute_boolean_operations() should be used as to factorize the corefinement operation, which makes up for the essential of the runtime.
The following basic example illustrates how to compute the union of two meshes:
Example: PMP_Boolean_operations/corefinement_mesh_union.cpp
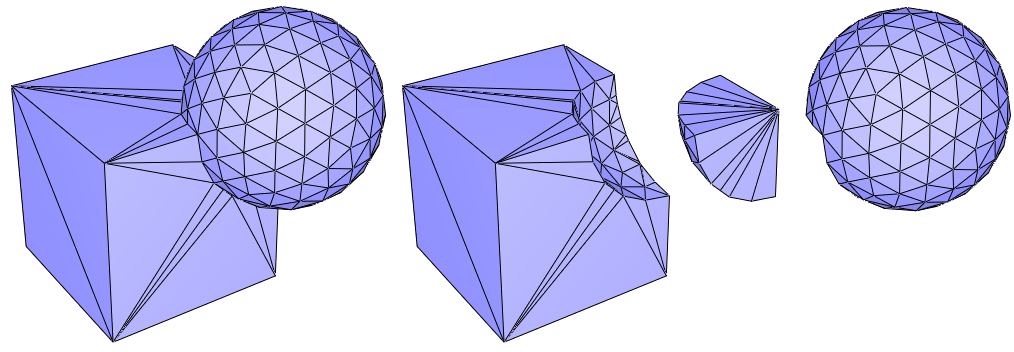
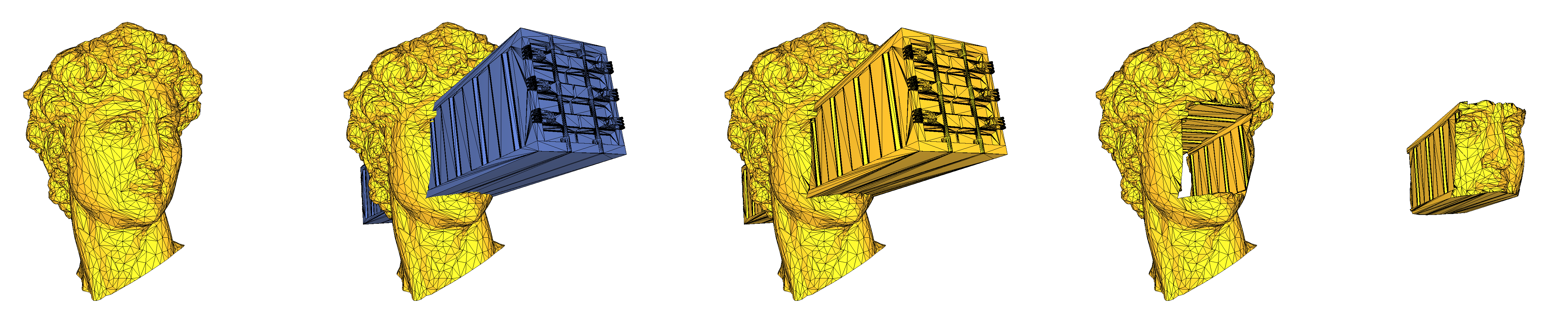
Figure 76.4 Let C and S be the volumes bounded by the triangulated surface meshes of a cube and a sphere, respectively. From left to right, the picture shows the triangulated surface meshes bounding the union of C and S, C minus S, the intersection of C and S, and S minus C.
There is no restriction on the topology of the input volumes. However, certain requirements must be met to ensure that the operation is feasible. First, the input meshes must be manifold triangulated surfaces bounding volumes. In particular, this means that they should not self-intersect. Second, the operation is only possible if the output can be bounded by a manifold triangulated surface mesh. In particular, this means that the output volume must not contain regions of zero thickness. Mathematically, the intersection with an infinitesimally small ball centered at any point of the output volume must be a topological ball. At the surface level, this means that no non-manifold vertex or edge is allowed in the output. For example, it is not possible to compute the union of two cubes that are disjoint but share an edge. If such scenarios arise, consider using the package 3D Boolean Operations on Nef Polyhedra. Alternatively, a special visitor (CGAL::Polygon_mesh_processing::Corefinement::Non_manifold_output_visitor) is provided for such cases and enables the user to get a triangle soup representing such a non-manifold output. See the example PMP_Boolean_operations/corefinement_mesh_non_manifold_intersection.cpp
It is possible to update the input so that it contains the result (in-place operation). In this case, the entire mesh is not copied; only the region around the intersection polyline is modified. However, note that if the Boolean operation is not possible, the input mesh will still be corefined.
If the input meshes contain triangles that are coplanar, it is guaranteed that the triangulations of those triangles in the two corefined meshes will be identical. Also all edges of those refined triangles will be reported as intersection edges (both in the function CGAL::Polygon_mesh_processing::surface_intersection() and in the named parameter edge_is_constrained_map() of corefine prefixed functions).
There is no restriction on the input for the function CGAL::Polygon_mesh_processing::autorefine_triangle_soup(). Degenerate triangles will be eliminated, duplicated points will be merged. If several triangles are coplanar, the output will contain as many copies of the triangulation of those refined triangles.
The minimal requirements of the corefinement based operations to terminate without crashing is to use a CGAL Kernel with exact predicates (such as CGAL::Exact_predicates_inexact_constructions_kernel). The graph structure is then always guaranteed to have the right topology as exact constructions are used internally. However, because of the rounding of the coordinates of the new intersection points, the embedding of the output surface meshes in the chosen kernel may feature self-intersections. This embedding issue goes away if a kernel with additionally exact constructions (such as CGAL::Exact_predicates_exact_constructions_kernel) is used. In particular, for consecutive operations, it is recommended to use a kernel with exact predicates and exact constructions.
From a user point of view, the choice of the kernel is done using the named parameter geom_traits(). If not provided, the kernel is deduced from the point type of the named parameter vertex_point_map(), which is by default the internal vertex point map of the mutable face graph used as input. If we take the example of CGAL::Surface_mesh<CGAL::Point_3<K>>, the kernel used will be K.
As for corefinement based operations described in the previous section, the function CGAL::Polygon_mesh_processing::autorefine_triangle_soup() requires a kernel with exact predicates in order to guarantee to terminate without issue. The output will then have the same topology as the exact output (for a triangle soup this means the indexed points and triangles will be the same as if exact computations were used). If non-exact constructions are used, points will be naively rounded and self-intersection might be created. In order to avoid that, we provide a robust heuristic that can be enabled using the named parameter apply_iterative_snap_rounding(). When set to true, it ensures that coordinates are rounded to fit in double with potential additional subdivisions, preventing self-intersections.
The following table illustrates the strength of the approach over the 10 000 models of the Thingi10k data set, demonstrating that naive rounding to floating point types is insufficient and fails to eliminate all self-intersections despite autorefinement, whereas the combination of autorefinement and iterative snap rounding resolves all of them on all meshes:
| Inputs with self-intersections | Autorefinement with naive rounding | Autorefinement with iterative snap rounding | ||
| 3870 | 529 | 0 | ||
This example is similar to the previous one, but here we subtract a volume and update the first input triangulated surface mesh (in-place operation). The edges that are on the intersection of the input meshes are marked and the region around them is remeshed isotropically while preserving the intersection polyline.
Example: PMP_Boolean_operations/corefinement_difference_remeshed.cpp
This example computes the intersection of two volumes and then performs the union of the result with one of the input volumes. This operation is in general not possible when using inexact constructions. Instead of using a mesh with points from a kernel with exact constructions, the exact points are stored as a property of the mesh vertices and can be reused in later operations. With this property, it is possible to manipulate a mesh with points having floating point coordinates while benefiting from the robustness provided by exact constructions.
Example: PMP_Boolean_operations/corefinement_consecutive_bool_op.cpp
The corefinement of two meshes can be also used to provide clipping functionalities with a volume bounded by a closed mesh and a clipper. The clipper can be a plane, a box, or another closed mesh. For example, in the case of plane clipping, the input mesh is corefined with the plane, and all parts of the mesh lying on the negative side of the plane are retained. Alternatively, one may choose not to discard any part, but simply split the input according to a plane, box, or mesh. This operation is called splitting.
The functions implementing these operations are:
Both functions offer options to select whether clipping should be performed at the volume or surface level, and whether the clipper should be considered compact. This is illustrated in Figure 76.5 and Figure 76.6.
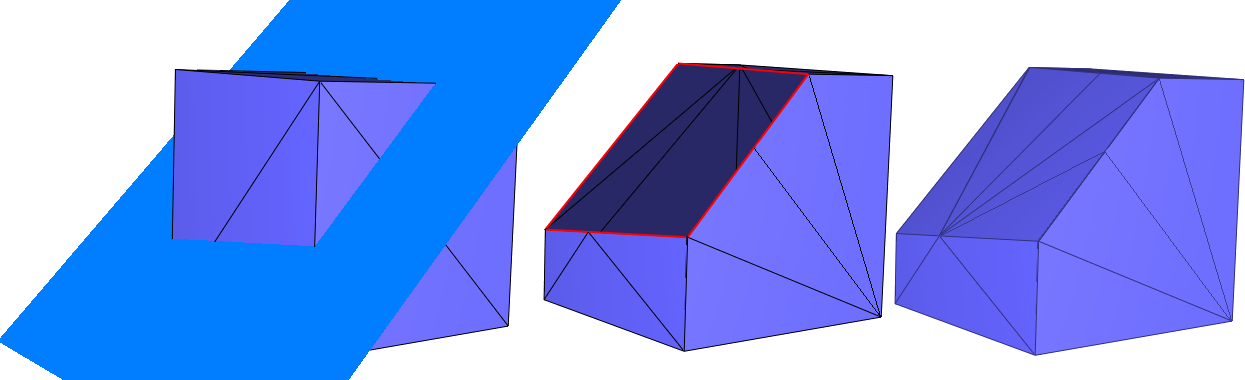
Figure 76.5 Clipping a cube with a halfspace. From left to right: (i) initial cube and the plane defining the clipping halfspace; (ii) clip_volume=false: clipping of the surface mesh (boundary edges depicted in red); (iii) clip_volume=true: clipping of the volume bounded by the surface mesh.
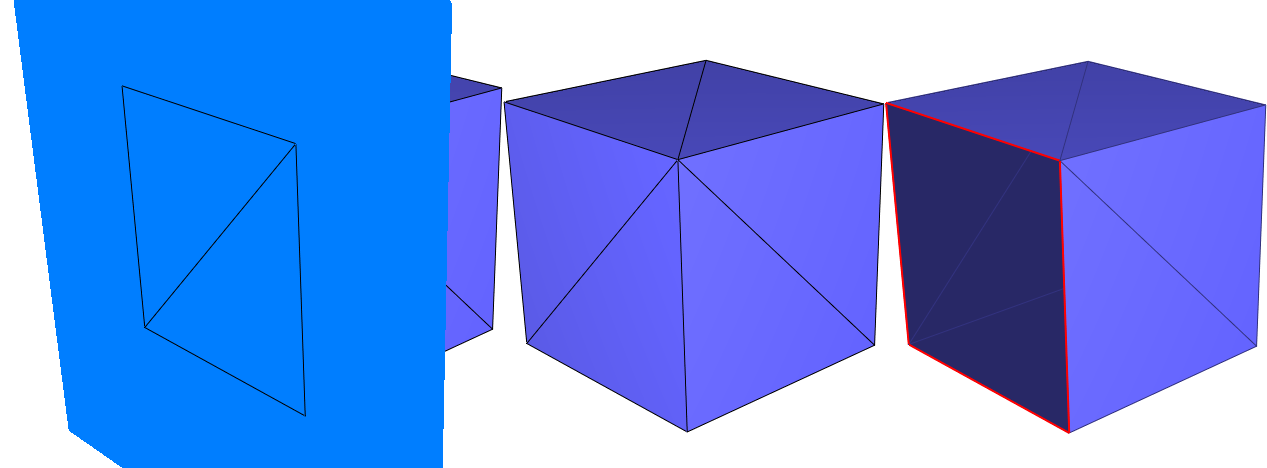
Figure 76.6 Clipping a cube with a halfspace: compactivity of the clipper (clip_volume=false in both cases). From left to right: (i) initial cube and the plane defining the clipping halfspace, note that a whole face of the cube (2 triangles) is exactly contained in the plane; (ii) use_compact_clipper=true: clipping of the surface mesh with a compact halfspace: coplanar faces are part of the output; (iii) use_compact_clipper=false: clipping of the surface mesh with a non-compact halfspace: coplanar faces are not part of the output.
The CGAL::Polygon_mesh_slicer is an operator that intersects a triangle surface mesh with a plane. It records the intersection as a set of polylines since the intersection can be made of more than one connected component. The degenerate case where the intersection is a single point is also handled.
Figure 76.7 shows the polylines returned by the slicing operation for a triangle mesh and a set of parallel planes.
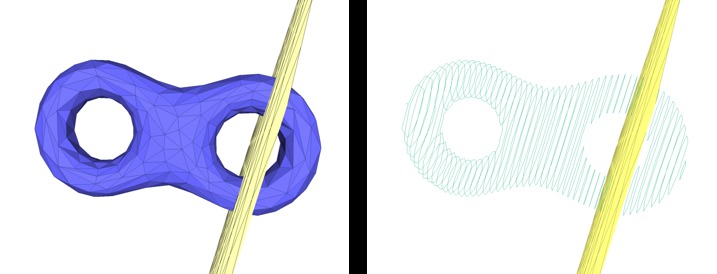
Figure 76.7 Slicing a mesh. A triangle mesh (left) and the polylines computed by the mesh slicer by intersecting a set of parallel planes (right).
The example below illustrates how to use the mesh slicer for a given triangle mesh and a plane. Two constructors are used in the example for pedagogical purposes.
Example: PMP_Boolean_operations/mesh_slicer_example.cpp
The kernel of a mesh is defined as the set of points from which the entire (oriented) surface of the mesh is visible. More formally, a point belongs to the kernel if, for every point on the mesh, the segment connecting them lies inside the mesh. Equivalently, the kernel is the intersection of all the half-spaces on the negative side of the oriented supporting planes of the faces of the mesh.
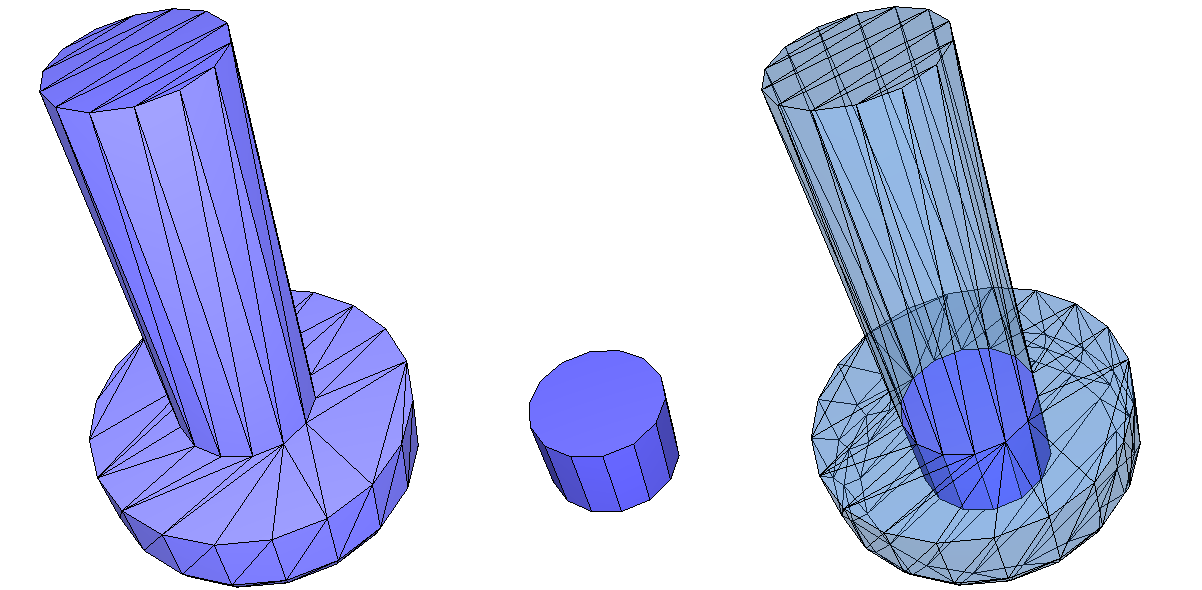
Figure 76.8 Mesh kernel: From left to right: (i) The input mesh; (ii) The kernel of the input; (iii) The kernel inside the mesh. All segments between a point of the kernel and a point of the mesh are inside the mesh.
The functions CGAL::Polygon_mesh_processing::kernel(), CGAL::Polygon_mesh_processing::kernel_point() and CGAL::Polygon_mesh_processing::has_empty_kernel() output the full kernel, a single point inside it or a Boolean indicating whether the kernel exists or not, respectively.
Corefinement was introduced in CGAL 4.10 by Sébastien Loriot.
The apply_iterative_snap_rounding option for autorefinement was developed by Sylvain Lazard and Léo Vaque [2], and implemented by Léo Valque in 2025.
The kernel functions and the specialization of clipping and plane refinement to convex inputs were implemented in 2025 by Léo Valque, inspired by the work of Sorgente et al. [1].