User Manual

Author

Qijia Huang

Figure 83.1 Medial skeleton of a bug model. Given a triangulated mesh(left), the medial skeleton is extracted, where each vertex corresponds a sphere(middle) and the connectivity of these spheres constructs a mesh(right) known as Medial mesh

Introduction

The skeleton is a fundamental structure with numerous applications in shape matching, shape segmentation, shape deformation, etc. A generalization of the skeleton is the medial axis, defined as the set of points that are equidistant to two or more points on the boundary of a shape. In this context, each point of the medial axis can be viewed as the center of a maximal inscribed ball, often referred to as a medial sphere.

This package implements a skeletonization algorithm [1] that extracts a coarse, discrete approximation of the medial axis from a triangulated surface mesh without borders. Unlike the Surface_mesh_skeletonization package, which computes a purely curve-based (1D) skeleton, the output of this method is a non-manifold triangle mesh that may contain both curve (1D) and surface (2D) elements, a structure sometimes referred to as a medial mesh. Each vertex of the resulting mesh corresponds to a medial sphere, and the edges and faces encode the adjacency relationships between these spheres. One can reconstruct the original mesh by interpolating between spheres according their adjacency relationships. For each edge, interpolating between two spheres yields a medial cone. For each face, interpolating between three spheres yields a medial slab.

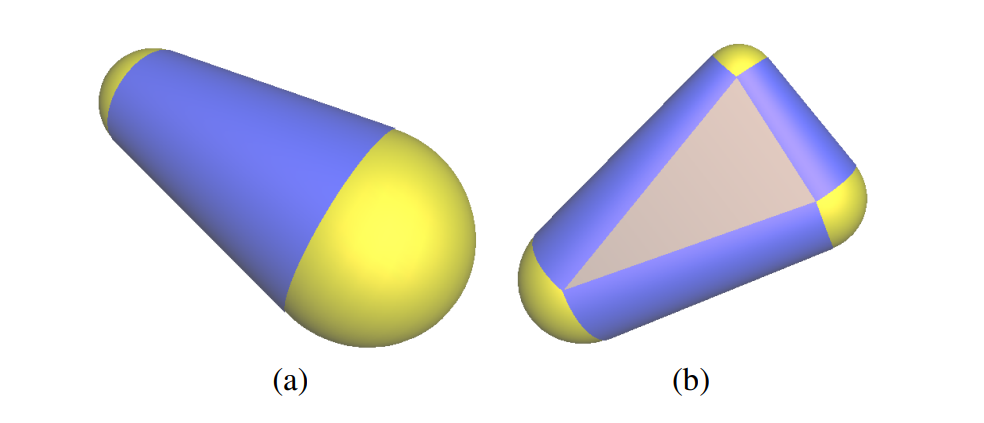
Figure 83.2 Interpolation of medial mesh. (a) medial cone (b) medial slab. Image taken from [2]

Overview

At the core of the method is a variational optimization problem whose objective is to minimize an error metric that measures the distance between each medial sphere and its associated surface points(cluster vertices), so that each sphere accurately represents the local geometry of the shape.

The process begins by initializing a single cluster containing all surface vertices and fitting an initial medial sphere using the variational error metric. New spheres are then progressively inserted in regions with the highest approximation error. Each insertion triggers updates to both the cluster vertices and the set of medial spheres in an iterative optimization loop. The algorithm terminates when either the target number of spheres is reached or the maximum number of iterations is exceeded. Finally, the connectivity of the medial skeleton is constructed based on the adjacency relations between vertex clusters.

Figure 83.3 Overview of the algorithm, image taken from [1]

User Interface Description

Input and Output

The method takes as input triangulated surface mesh which can be a mode of FaceListGraph, such as CGAL::Surface_mesh. It also requires Eigen (version 3.2 or later) for the use of the Eigen::LDLT solver, which is employed to solve the linear systems arising during optimization.

The output is stored in a Medial_skeleton structure, which contains three containers:

• vertices: each element corresponds to a medial sphere,
• edges: each element is a std::pair<std::size_t, std::size_t> encoding the adjacency between two spheres,
• faces: each element is a triplet of Sphere_ID(std::array<std::size_t, 3>) values encoding a triangular patch connecting three spheres.

A helper function CGAL:IO::write_PLY() is provided to export the resulting skeleton to a .ply file, which can then be visualized in external software such as Blender.

Acceleration Structure

After the optimization step, the medial spheres may deviate slightly from the true medial axis. To project them back onto the medial axis, the algorithm performs a correction step using the shrinking ball algorithm,[3] which requires computing the closest point on the surface from a given position.

To accelerate this closest point query, two types of spatial search structures are supported:

• CGAL::KD_tree_tag: uses a KD-tree constructed from the surface sample points.
• CGAL::BVH_tag: uses a bounding volume hierarchy (BVH) built from the faces of the input triangle mesh.

The user can choose the desired structure by passing the corresponding tag via the CGAL::parameters::acceleration_structure() named parameter. The essential difference is that the KD-tree restricts sphere placement to be constrained by surface sampled points only, while the BVH allows medial spheres to touch the interior of mesh faces. In general, we recommend using the KD-tree (which is also the default) since the surface will be densely sampled at the beginning of the algorithm.

Free function

The function CGAL::extract_variational_medial_skeleton() provides a convenient interface for users who want to quickly extract a medial skeleton with specified parameters. This function accepts the following parameters:

• number_of_spheres: target number of medial spheres
• number_of_samples: number of points that will be sampled on the surface
• lambda: weight balancing the energy terms
• random_seed: random seed for generating sample points on the surface
• number_of_iterations: maximum number of iterations
• concurrency_tag: execution mode - sequential or parallel

The following example showcases the usage of this function:

File Variational_medial_axis/vmas_free_function.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/extract_variational_medial_skeleton.h>
 
using K = CGAL::Exact_predicates_inexact_constructions_kernel;
using Mesh = CGAL::Surface_mesh<K::Point_3>;
using Medial_skeleton = CGAL::Medial_skeleton<Mesh>;
 
int main(int argc, char** argv)
{
  const std::string filename = (argc > 1) ? argv[1] : CGAL::data_file_path("meshes/elephant.off");
 
  Mesh mesh;
  if(!CGAL::IO::read_polygon_mesh(filename, mesh))
  {
    std::cerr << "Invalid input." << std::endl;
    return 1;
  }
 
  Medial_skeleton skeleton = extract_variational_medial_skeleton(
      mesh, CGAL::parameters::number_of_iterations(1000)// number of max iterations
      .number_of_spheres(200) // target number of spheres
      .number_of_samples(20000) // number of surface samples
      .lambda(0.2) // lambda parameter for the optimization
      .random_seed(10) // random seed for point sampling
      .concurrency_tag(CGAL::Parallel_tag{}) // use parallel execution
      .acceleration_structure(CGAL::BVH_tag{}) // use BVH for acceleration
      .verbose(true)); // enable verbose output
  // Write skeleton to PLY file
  std::string output_filename = "skeleton.ply";
  CGAL::IO::write_PLY(skeleton, output_filename, CGAL::parameters::stream_precision(9));
 
}

Function object

The class CGAL::Variational_medial_axis_sampling provides some advanced usage of the algorithm Several key functions are provided for algorithm control:

• CGAL::Variational_medial_axis_sampling::sample(): Executes the complete algorithm with specified parameters and returns a boolean indicating success. The algorithm may fail either when the optimization does not converge (the error stays above the error threshold) or when the surface sampling is not dense enough to generate a sufficient number of medial spheres. The parameters are the same as those of the free function.
• CGAL::Variational_medial_axis_sampling::update_single_step(): Performs a single iteration of the optimization process, with optional sphere splitting enabled. This allows for step-by-step execution and monitoring of the algorithm's progress.
• CGAL::Variational_medial_axis_sampling::update(): Executes a specified number of optimization iterations without sphere splitting.
• CGAL::Variational_medial_axis_sampling::add_spheres(int nb_spheres): Adds a specified number of spheres by iteratively splitting existing spheres.

The following example shows a different configuration of the parameters and basic usage of the above functions:

File Variational_medial_axis/vmas_class_interface.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Surface_mesh.h>
#include <CGAL/Variational_medial_axis_sampling.h>
 
using K = CGAL::Exact_predicates_inexact_constructions_kernel;
using Mesh = CGAL::Surface_mesh<K::Point_3>;
 
int main(int argc, char** argv)
{
  const std::string filename = (argc > 1) ? argv[1] : CGAL::data_file_path("meshes/chair.off");
 
  Mesh mesh;
  if(!CGAL::IO::read_polygon_mesh(filename, mesh))
  {
    std::cerr << "Invalid input." << std::endl;
    return 1;
  }
 
  CGAL::Variational_medial_axis_sampling<Mesh, CGAL::Parallel_if_available_tag> vmas(mesh);
  // Compute medial skeleton with custom parameters
  vmas.sample(
      CGAL::parameters::number_of_iterations(1000) // number of max iterations
      .number_of_spheres(200)// target number of spheres
      .lambda(0.2) // lambda parameter for the optimization
      .verbose(true)); // enable verbose output
 
  // add additional 3 sphere, this function will update the medial skeleton automatically
  vmas.add_spheres(3);
  // update the medial skeleton with 20 iterations
  vmas.update(20);
 
  std::cout << "Exporting skeleton..." << std::endl;
  auto skeleton = vmas.skeleton();
 
  // Write skeleton to PLY file
  std::string output_filename = "skeleton.ply";
  CGAL::IO::write_PLY(skeleton, output_filename, CGAL::parameters::stream_precision(9));
 
}
 

Limitations and Practical Considerations

By definition, the medial axis of a shape is homotopy equivalent to the original object. However, since this algorithm aims to generate coarse approximation of medial axis, it does not provide any theoretical guarantee that the extracted skeleton preserves the topology of the input. While the algorithm can handle meshes with multiple connected components, the resulting medial skeleton is only topologically faithful when a sufficient number of spheres is used to capture the correct connectivity. Furthermore, this method does not perform well on CAD models, which typically require additional feature detection to preserve sharp features.

Design and Implementation History

This package is the result of the work of Qijia Huang during the 2025 season of the Google Summer of Code, mentored by Sébastien Loriot.