#include <CGAL/HDVF/Cubical_chain_complex.h>

Definition

template<typename CoefficientRing, typename Traits>
class CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >

The class Cubical_chain_complex represents (topological) chain complexes associated to cubical complexes.

Description

A cubical complex is a set of "square" cells such that: all the faces of a given cell also belong to the complex and any two cells intersect exactly along a common face.

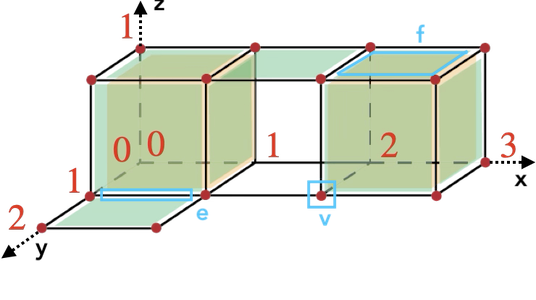
A cell in a cubical complex of dimension q is the cartesian product of \(q\) intervals \([n_1,n_1+\delta_1]\times [n_q,n_q+\delta_q] \) with \(n_i\in \mathbb N \) and \(\delta_i = 0,1\). The dimension of such a cell is \(\sum_{i=1}^q \delta_i\). A 0-cell is thus a vertex, a 1-cell contains one non zero delta (edge along one of the axes), a 2-cell contains two non zero deltas (square along two of the axes), while a 3-cell is a cube...

For instance, \(v = [2,2]\times[1,1]\times[0,0]\), \(e = [0,1]\times[1,1]\times[0,0]\) and \(f = [2,3]\times[0,1]\times[1,1]\).

Given a cubical complex of dimension \(q\) included in \([0,B_1]\times\cdots \times[0,B_q]\), Khalimsky coordinates associate to each cell of the complex a unique coordinate in \([0,2B_1]\times\cdots \times[0,2B_q]\):

\[ \begin{array}{rcl} \sigma & \mapsto & \mathrm{khal}(\sigma) \\ [n_1,n_1+\delta_1]\times\cdots \times [n_q,n_q+\delta_q] & \,\to\, & (2n_1+\delta_1,\ldots,2n_1+\delta_1) \\ \end{array}\]

we set \(N_i = 2B_i+1\) the size of the Khalimsky bounding box along the \(i\)th axis.

The dimension of a cell is the given by the number of odd coordinates. In our previous example, \(B_1=3, B_2=2, B_3=1\), hence \(N_1=7, N_2=5, N_3=3\) and we get the following Khalimsky coordinates: \(\mathrm{khal}(v) = (4,2,0)\), \(\mathrm{khal}(e) = (1,2,0)\) and \(\mathrm{khal}(f) = (5,1,2)\).

The boundary map of the complex is computed by the constructor of the class using the standard formula with Khalimsky coordinates. Given a cell \(\sigma\) with \(\mathrm{khal}(\sigma) = (x_1,\ldots,x_q)\)

\[ \partial(x_1,\ldots,x_q) = \sum_{\substack{i=0\\x_i\text{ odd}}}^q (-1)^{j(i)} \left( (x_1,\ldots,x_i+1,\ldots, x_q) - (x_1,\ldots,x_i-1,\ldots, x_q)\right)\]

where \(j(i)\) is the number of odd coordinates between \(x_1\) and \(x_i\).

Let us also point out that besides Khalimsky coordinates, cells are indexed along each dimension, thus each cell is uniquely determined by its dimension and its index in this dimension (called "base index").

Implementation Details

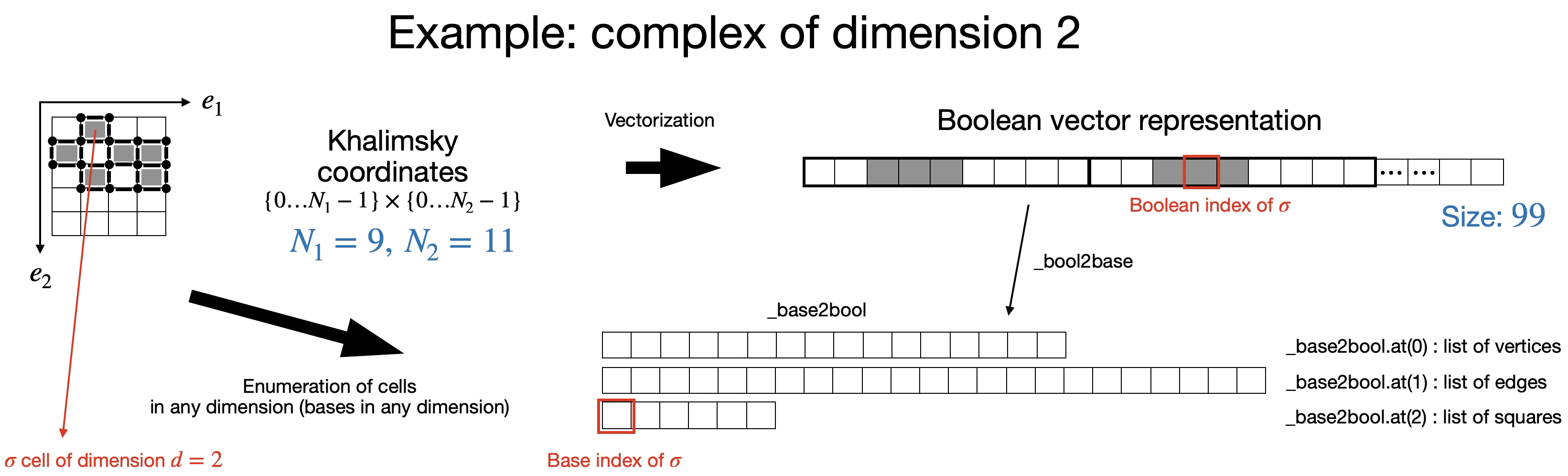
As described above, Khalimsky coordinates provide a convenient tool to identify cells of any dimension. Hence a complex of dimension \(q\) can be encoded by a Boolean matrix of size \(N_1\times\cdots\times N_q\) (with previous notations). For convenience, this matrix is vectorized and thus the complex is stored in a Boolean vector (denoted by _cells) of size \(N_1\times \cdots \times N_q\).

Cells of any dimension are thus repesented by a given element of this Boolean vector and the corresponding index is called their Boolean index.

As stated above, besides this Boolean representation, topological computations require to identify the bases of cells in any dimension (bases of the free chain groups). Hence, a cell of dimension \(d\) is also identified by its index in the basis of \(d\)-dimensional cells. This index is called its basis index. The vector _bool2base stores, for each dimension, the map between Boolean and base indices, while the _base2bool stores, for each dimension, the permutation between base and Boolean indices.

Is model of: GeometricChainComplex

Template Parameters

CoefficientRing	a model of the `IntegralDomainWithoutDivision` concept.
Traits	a geometric traits class model of the `HDVFTraits` concept.

Public Types
enum	Cubical_complex_primal_dual { PRIMAL , DUAL }
	Type used to encode primal or dual construction. More...

typedef CoefficientRing	Coefficient_ring
	Type of coefficients used to compute homology.

typedef Traits::Point	Point
	Type of vertex coordinates.

typedef Traits::Point3	Point3
	Type of vtk export vertex coordinates.

typedef CGAL::OSM::Sparse_chain< CoefficientRing, CGAL::OSM::COLUMN >	Column_chain
	Type of column-major chains.

typedef CGAL::OSM::Sparse_chain< CoefficientRing, CGAL::OSM::ROW >	Row_chain
	Type of row-major chains.

typedef CGAL::OSM::Sparse_matrix< CoefficientRing, CGAL::OSM::COLUMN >	Column_matrix
	Type of column-major sparse matrices.

Public Member Functions
	Cubical_chain_complex ()
	Default constructor (empty cubical complex).

	Cubical_chain_complex (const Cub_object_io< Traits > &cub, Cubical_complex_primal_dual type)
	Constructor from a Cub_object_io (builds PRIMAL or DUAL associated complex depending on `type`).

Cubical_chain_complex &	operator= (const Cubical_chain_complex &complex)
	Assignment operator for cubical chain complexes.

Column_chain	d (size_t id_cell, int q) const
	Returns the boundary of the cell id_cell in dimension q.

Row_chain	cod (size_t id_cell, int q) const
	Returns the co-boundary of the cell id_cell in dimension q.

size_t	number_of_cells (int q) const
	Returns the number of cells in a given dimension.

int	dimension () const
	Returns the dimension of the complex.

std::vector< size_t >	size_bb () const
	Get the size of the Khalimsky bounding box.

size_t	size () const
	Returns the total size of the complex.

std::vector< size_t >	index_to_cell (size_t i, int q) const
	Returns Khalimsky coordinates of the cell of "basis index" i in dimension q.

size_t	cell_to_index (std::vector< size_t > cell) const
	Returns the "basis index" of a cell given by its Khalimsky coordinates.

int	dimension (const std::vector< size_t > &cell) const
	Returns the dimension of a cell (given in Khalimsky coordinates).

std::vector< size_t >	bindex_to_cell (size_t i) const
	Returns Khalimsky coordinates of the cell of Boolean index i.

size_t	cell_to_bindex (std::vector< size_t > cell) const
	Returns the Boolean index of a cell given by its Khalimsky coordinates.

const std::vector< Column_matrix > &	boundary_matrices () const
	Returns a constant reference to the vector of boundary matrices (along each dimension).

const Column_matrix &	boundary_matrix (int q) const
	Returns a copy of the dim-th boundary matrix (ie. column-major matrix of \(\partial_q\)).

std::vector< size_t >	bottom_faces (size_t id_cell, int q) const
	Returns dimension 0 cell indices included in the cell with index `id_cell` of dimension `q`.

template<typename CoefficientT , int ChainTypeF>
Column_chain	cofaces_chain (OSM::Sparse_chain< CoefficientT, ChainTypeF > chain, int q) const
	Returns the cofaces of a given chain in dimension `q`.

size_t	get_id () const
	Gets (unique) object Id.

Point	point (size_t i) const
	Gets the coordinates of the ith vertex.

const std::vector< Point > &	points () const
	Gets the vector of vertex coordinates

Static Public Member Functions
template<typename LabelType = int>
static void	chain_complex_to_vtk (const Cubical_chain_complex< CoefficientRing, Traits > &K, const std::string &filename, const std::vector< std::vector< LabelType > > *labels=NULL, std::string label_type_name="int")
	END Methods of the Cubical_chain_complex concept.

static void	chain_to_vtk (const Cubical_chain_complex< CoefficientRing, Traits > &K, const std::string &filename, const OSM::Sparse_chain< CoefficientRing, OSM::COLUMN > &chain, int q, size_t cellId=-1)

Protected Member Functions
std::ostream &	print_complex (std::ostream &out=std::cout) const
	Prints informations on the complex.

Point	compute_point (size_t i) const

void	compute_points ()

std::vector< size_t >	get_P () const

std::vector< bool >	get_cells () const

std::vector< std::vector< size_t > >	get_base2bool () const

std::vector< std::map< size_t, size_t > >	get_bool2base () const

Column_chain	boundary_cell (size_t index_base, int dim) const

bool	is_valid_cell (const std::vector< size_t > &cell) const

bool	is_valid_cell (size_t id_cell) const

std::vector< size_t >	khal_to_verts (std::vector< size_t > c) const

void	initialize_cells (const Cub_object_io< Traits > &cub, Cubical_complex_primal_dual type)

int	dimension (size_t cell_index) const

std::vector< size_t >	ind2vox (size_t index, std::vector< size_t > B, size_t max_size) const

size_t	vox2ind (const std::vector< size_t > &base_indices, std::vector< size_t > B, size_t max_size) const

void	compute_d (int q)

void	insert_cell (size_t cell)

std::vector< size_t >	compute_boundaries (size_t cell) const

Protected Attributes
int	_dim

std::vector< size_t >	_size_bb

std::vector< size_t >	_P

std::vector< bool >	_cells

std::vector< std::vector< size_t > >	_base2bool

std::vector< std::map< size_t, size_t > >	_bool2base

std::vector< Column_matrix >	_d

std::vector< Point >	_points

Friends
template<typename _CT , typename _Traits >
std::ostream &	operator<< (std::ostream &out, const Cubical_chain_complex< _CT, _Traits > &complex)
	Prints informations on the complex.

Member Enumeration Documentation

◆ Cubical_complex_primal_dual

template<typename CoefficientRing , typename Traits >

enum CGAL::Homological_discrete_vector_field::Cubical_chain_complex::Cubical_complex_primal_dual

Type used to encode primal or dual construction.

Enumerator
PRIMAL
DUAL

Constructor & Destructor Documentation

◆ Cubical_chain_complex() [1/2]

template<typename CoefficientRing , typename Traits >

CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::Cubical_chain_complex ( )

Default constructor (empty cubical complex).

Builds an empty cubical complex.

◆ Cubical_chain_complex() [2/2]

template<typename CoefficientRing , typename Traits >

CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::Cubical_chain_complex	(	const Cub_object_io< Traits > &	cub,
		Cubical_complex_primal_dual	type
	)

Constructor from a Cub_object_io (builds PRIMAL or DUAL associated complex depending on type).

Builds the cubical complex associated to a a set of cells (vertices, edges, squares, cubes...), ie. performs the down closure of cells and set the boundary matrices in any dimension. Given a set of cells:

if the type is PRIMAL, the constructor builds the associated complex as such (see below middle), which comes to encode \(3^q-1\) connectivity (with \(q\) the dimension of the complex)
if the type is DUAL and the Cub_object_io contains only cells of maximal dimension (ie. binary object), the constructor build the dual associated complex (see below right), which comes to encode \(2q\) connectivity (with \(q\) the dimension of the complex)

Parameters

cub	A Cub_object_io containing a set of "cubical" cells.
type	Type of construction used (PRIMAL or DUAL).

Member Function Documentation

◆ bindex_to_cell()

template<typename CoefficientRing , typename Traits >

std::vector< size_t > CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::bindex_to_cell ( size_t i ) const

Returns Khalimsky coordinates of the cell of Boolean index i.

In Cubical_chain_complex, a cells of dimenson q, besides its index in the basis of \(q\)-cells, has an index in the vectorisation of the Khalimsky representation, called its "Boolean index" (see above).

Parameters

i	The "Boolean" index of a cell.

Returns: Khalimsky coordinates of the cell.

◆ bottom_faces()

template<typename CoefficientRing , typename Traits >

std::vector< size_t > CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::bottom_faces	(	size_t	id_cell,
		int	q
	)		const

Returns dimension 0 cell indices included in the cell with index id_cell of dimension q.

Returns the dimension 0 vertex indices included in the cell with index id_cell of dimension q.

Parameters

id_cell	Index of the cell.
q	Dimension of the cell.

Returns: A vector of 0-cell indices.

◆ boundary_matrices()

template<typename CoefficientRing , typename Traits >

const std::vector< Column_matrix > & CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::boundary_matrices ( ) const

Returns a constant reference to the vector of boundary matrices (along each dimension).

Returns a constant reference to the vector of boundary matrices along each dimension. The q-th element of this vector is a column-major sparse matrix containing the boundaries of q-cells (ie. rows encode q-1 cells and columns q cells).

Returns: Returns a constant reference to the vector of column-major boundary matrices along each dimension.

◆ boundary_matrix()

template<typename CoefficientRing , typename Traits >

const Column_matrix & CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::boundary_matrix ( int q ) const

Returns a copy of the dim-th boundary matrix (ie. column-major matrix of \(\partial_q\)).

It is a column-major sparse matrix containing the boundaries of dim-cells (ie. rows encode q-1 cells and columns q cells).

Parameters

q	Dimension of the boundary matrix (ie. columns will contain the boundary of dimension q cells).

Returns: A column-major sparse matrix containing the matrix of the boundary operator of dimension q.

◆ cell_to_bindex()

template<typename CoefficientRing , typename Traits >

size_t CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::cell_to_bindex ( std::vector< size_t > cell ) const

Returns the Boolean index of a cell given by its Khalimsky coordinates.

In Cubical_chain_complex, a cells of dimenson q, besides its index in the basis of \(q\)-cells, has an index in the vectorisation of the Khalimsky representation, called its "Boolean index" (see above).

Parameters

cell	Khalimsky coordinates of a cell.

Returns: The "Boolean" index of the cell.

◆ cell_to_index()

template<typename CoefficientRing , typename Traits >

size_t CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::cell_to_index ( std::vector< size_t > cell ) const

Returns the "basis index" of a cell given by its Khalimsky coordinates.

In AbstractChainComplex, cells of dimenson q are identified by their index in the basis of \(q\)-cells together with their dimension. In the context of cubical complexes, this index is called "basis index" (to distinguish from its "Boolean index", see above).

Parameters

cell	Khalimsky coordinates of a cell (of dimension \(q\)).

Returns: The "basis index" of the cell among \(q\)-cells.

◆ cod()

template<typename CoefficientRing , typename Traits >

Row_chain CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::cod	(	size_t	id_cell,
		int	q
	)		const

Returns the co-boundary of the cell id_cell in dimension q.

Returns a row-major chain containing the co-boundary of the cell id_cell in dimension q (so actually a row of the boundary matrix).

Warning: As the boundary matrix is stored column-major, this entails crossing the full matrix to extract the row coefficients (O(number of non empty columns))

Parameters

id_cell	Index of the cell.
q	Dimension of the cell.

Returns: The row-major chain containing the co-boundary of the cell id_cell in dimension q.

◆ cofaces_chain()

template<typename CoefficientRing , typename Traits >

template<typename CoefficientT , int ChainTypeF>

Column_chain CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::cofaces_chain	(	OSM::Sparse_chain< CoefficientT, ChainTypeF >	chain,
		int	q
	)		const

Returns the cofaces of a given chain in dimension q.

The resulting chain lies in dimension q+1 and is null if this dimension exceeds the dimension of the complex.

◆ d()

template<typename CoefficientRing , typename Traits >

Column_chain CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::d	(	size_t	id_cell,
		int	q
	)		const

Returns the boundary of the cell id_cell in dimension q.

Returns a copy of the column-major chain stored in the boundary matrix of dimension q: boundary of the cell id_cell in dimension q.

Parameters

id_cell	Index of the cell.
q	Dimension of the cell.

Returns: The column-major chain containing the boundary of the cell id_cell in dimension q.

◆ dimension()

template<typename CoefficientRing , typename Traits >

int CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::dimension ( ) const

Returns the dimension of the complex.

Returns the dimension of the cubical complex.

Returns: The dimension of the complex..

◆ get_id()

template<typename CoefficientRing , typename Traits >

size_t CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::get_id ( ) const

Gets (unique) object Id.

For comparison of constant references to the complex.

◆ index_to_cell()

template<typename CoefficientRing , typename Traits >

std::vector< size_t > CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::index_to_cell	(	size_t	i,
		int	q
	)		const

Returns Khalimsky coordinates of the cell of "basis index" i in dimension q.

In AbstractChainComplex, cells of dimenson q are identified by their index in the basis of \(q\)-cells together with their dimension. In the context of cubical complexes, this index is called "basis index" (to distinguish from its "Boolean index", see above).

Parameters

i	"basis index" of a cell.
q	dimension of the cell.

Returns: Khalimsky coordinates of the cell.

◆ number_of_cells()

template<typename CoefficientRing , typename Traits >

size_t CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::number_of_cells ( int q ) const

Returns the number of cells in a given dimension.

Parameters

q	Dimension along which the number of cells is returned.

Returns: Number of cells in dimension q.

◆ operator=()

template<typename CoefficientRing , typename Traits >

Cubical_chain_complex & CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::operator= ( const Cubical_chain_complex< CoefficientRing, Traits > & complex )

Assignment operator for cubical chain complexes.

Stores a copy of an cubical chain complex in *this.

Parameters

complex The cubical chain complex which will be copied.

◆ print_complex()

template<typename CoefficientRing , typename Traits >

std::ostream & CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::print_complex ( std::ostream & out = std::cout ) const

protected

Prints informations on the complex.

Displays the number of cells in each dimension and the boundary matrix in each dimension.

◆ size()

template<typename CoefficientRing , typename Traits >

size_t CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::size ( ) const

Returns the total size of the complex.

Khalimsky coordinates in dimension q are bounded above by size_bb().at(q); the total memory size of the complex is the product of these sizes.

◆ size_bb()

template<typename CoefficientRing , typename Traits >

std::vector< size_t > CGAL::Homological_discrete_vector_field::Cubical_chain_complex< CoefficientRing, Traits >::size_bb ( ) const

Get the size of the Khalimsky bounding box.

The Khalimsky coordinate of a cell c in dimension q is strictly lesser than size_bb().at(q).

Friends And Related Function Documentation

◆ operator<<

template<typename CoefficientRing , typename Traits >

template<typename _CT , typename _Traits >

std::ostream & operator<<	(	std::ostream &	out,
		const Cubical_chain_complex< _CT, _Traits > &	complex
	)

friend

Prints informations on the complex.

Displays the number of cells in each dimension and the boundary matrix in each dimension.

Definition

Description

Implementation Details

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Protected Attributes

Friends

Member Enumeration Documentation

◆ Cubical_complex_primal_dual

Constructor & Destructor Documentation

◆ Cubical_chain_complex() [1/2]

◆ Cubical_chain_complex() [2/2]

Member Function Documentation

◆ bindex_to_cell()

◆ bottom_faces()

◆ boundary_matrices()

◆ boundary_matrix()

◆ cell_to_bindex()

◆ cell_to_index()

◆ cod()

◆ cofaces_chain()

◆ d()

◆ dimension()

◆ get_id()

◆ index_to_cell()

◆ number_of_cells()

◆ operator=()

◆ print_complex()

◆ size()

◆ size_bb()

Friends And Related Function Documentation

◆ operator<<