Author: Ken Arroyo Ohori

Introduction

This package implements polygon repair methods. Starting from possibly invalid input in the form of a polygon, polygon with holes or multipolygon with holes, the method computes an arrangement of the input edges, labels each face according to what it represents (exterior, polygon interior or hole), and reconstructs the polygon(s) represented by the arrangement. The method returns valid output stored in a multipolygon with holes.

Different labeling heuristics are possible. This package offers the even-odd rule, the non-zero rule, the union rule, as well as the intersection rule. The even-odd rule results in areas that are alternately assigned as polygon interiors and exterior/holes each time that an input edge is passed. It does not distinguish between edges that are part of outer boundaries from those of inner boundaries. The non-zero rule results in areas with a non-zero winding number. The union and intersection rules are useful when given two or more similar valid polygons with holes. They compute either their union or their intersection, and they are hence conservative by bounding from the interior or the exterior.

Definitions

A valid polygon (without holes) is a point set in \( \mathbb{R}^2\) that is bounded by a cycle of linear edges, which is known as its outer boundary. This outer boundary should be simple, meaning that the interiors of its edges are pairwise disjoint and all of its vertices have a degree of two. It is thus topologically equivalent to a disk and is represented internally as the sequence of points at the common end points of the edges around its outer boundary.
A valid polygon with holes is a point set in \( \mathbb{R}^2\) that is bounded by one outer boundary and zero or more inner boundaries, where each inner boundary represents a hole in the polygon. Considered independently, each boundary should be simple. The different boundaries of a polygon are allowed to intersect tangentially at their common vertices (with no common edges), forming vertices with degrees of a multiple of two the tangential points. The interior of a polygon with holes should form a connected point set. Note that a valid polygon can also be represented as a valid polygon with holes (where the number of holes is zero).
A valid multipolygon with holes is a point set in \( \mathbb{R}^2\) that is represented by a set of zero or more valid polygons with holes. The interiors of the polygons with holes should be pairwise disjoint, but they are allowed to intersect tangentially at their common vertices. Note that a valid polygon with holes can also be represented as a valid multipolygon with holes (with only one polygon).

Figure 16.1 Valid: (a) polygon, (b-c) polygons with holes, and (d-e) multipolygons with holes. (c) and (e) show cases where boundaries intersect tangentially at a single vertex.

Figure 16.2 Invalid: (a) self-intersecting polygon self-intersection, (b) self-touching polygon, (c-d) polygons with badly nested holes, (e) polygon with hole touching at edge, (f) polygon with hole that separates interior into two parts, (g) multipolygon with overlapping polygons, and (h) multipolygon with polygons that touch at an edge.

Even-Odd and Non-Zero Rule

While the even-odd rule switches between inside/outside at each edge only taking into account multiplicity, the non-zero rule takes also into account the orientation of the edge.

For some configurations this leads to different results, as can be seen in the figure below.

Figure 16.3 Input (left), non-zero (middle) even-odd (right).

And there are other configurations where the two rules lead to the same result.

Figure 16.4 Input (left), non-zero and even-odd (right).

A valid polygon with holes, obviously has the same result with both rules applied as it is just the identity. However an invalid multipolygon with one polygon enclosing the other one results in the union of the two, that is the enclosing one for the non-zero rule, while it results in a polygon with hole for the even-odd rule.

Figure 16.5 Input (left), non-zero (middle) even-odd (right).

Union and Intersection Rule

Given several valid polygons this rule computes their union or intersection. This approximates from outside and from inside, respectively.

Figure 16.6 Union (top) and Intersection (bottom).

Notes on the Output

The conditions listed above are sufficient to define valid polygons, polygons with holes and multipolygons with holes for most applications. However, in order to ensure unique deterministic output from the repair algorithm, the valid multipolygons with holes returned by the package conform to more strict criteria:

Adjacent collinear edges touching at vertices of degree two are merged
The sequence of vertices representing a boundary starts from its lexicographically smallest vertex
Outer boundaries are oriented counter-clockwise and inner boundaries are oriented clockwise
The inner boundaries of a polygon with holes are stored in lexicographic order
The polygons with holes of a multipolygon with holes are also stored in lexicographic order

If the input is already valid, the method will return a valid output representing the same area. However, the output might be different in order to conform to the stricter conditions to generate deterministic output.

Also, it is worth noting that even the repair of a single polygon without holes but with self-intersections can result in a multipolygon with holes. This is why the repair function will always return a multipolygon with holes. The user can then check whether it consists of a single polygon with holes, and if a polygon with holes has zero holes and extract these if needed.

Examples

Repairing a (Multi)polygon with the Even-Odd Rule

It is possible to repair a polygon, polygon with holes or multipolygon with holes using the even-odd rule by calling the Polygon_repair::repair() function as shown in the following example. This function returns a repaired multipolygon with holes.

File Polygon_repair/repair_polygon_2.cpp

#include <iostream>
#include <fstream>
#include <string>
 
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Polygon_repair/repair.h>
#include <CGAL/IO/WKT.h>
 
using Kernel = CGAL::Exact_predicates_inexact_constructions_kernel;
using Point_2 = Kernel::Point_2;
using Polygon_2 = CGAL::Polygon_2<Kernel>;
using Polygon_with_holes_2 = CGAL::Polygon_with_holes_2<Kernel>;
using Multipolygon_with_holes_2 = CGAL::Multipolygon_with_holes_2<Kernel>;
 
int main(int argc, char* argv[]) {
 
  const char* filename = (argc > 1) ? argv[1] : "data/bridge-edge.wkt";
 
  std::ifstream in(filename);
  Polygon_with_holes_2 pin;
  CGAL::IO::read_polygon_WKT(in, pin);
 
  Multipolygon_with_holes_2 mp = CGAL::Polygon_repair::repair(pin);
  if (mp.number_of_polygons_with_holes() > 1) {
    CGAL::IO::write_multi_polygon_WKT(std::cout, mp);
  } else {
    CGAL::IO::write_polygon_WKT(std::cout, mp.polygons_with_holes()[0]);
  }
 
  return 0;
}

Performance

The method can repair large invalid polygons of millions of vertices in a few seconds as long as the number of intersections between line segments is limited. This is a realistic assumption with many invalid data sets, which only have relatively minor issues involving a small number of their vertices/edges. However, it is worth noting that there can be a potentially quadratic number of intersection between edges in the worst case, leading to much worse performance since all of these intersections need to be calculated in the overlay.

Polygon	Vertices	Holes	Time
	101973	298	0.652 sec
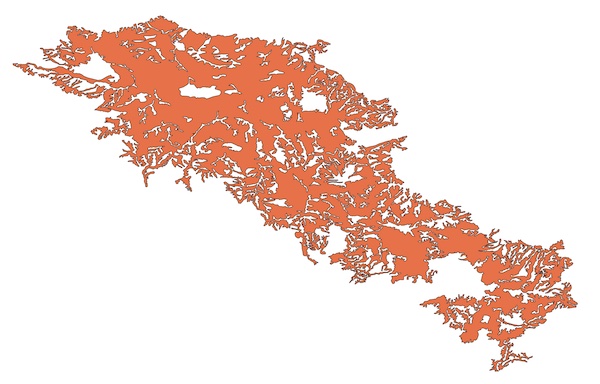	43925	125	0.190 sec

History

The polygon repair method as originally developed is described by Ledoux et al. [1] and implemented in the prepair software. This package is a reimplementation of the method with a new approach to label and reconstruct the multipolygons. It also incorporates improvements later added to prepair, such as the application of the even-odd counting heuristics to edges, which enables correct counting even on partially overlapping edges.

Ken Arroyo Ohori developed this package during the Google Summer of Code 2023 mentored by Sébastien Loriot and Andreas Fabri. The GSoC project was limited to the even-odd rule. Further rules were added with CGAL 6.1 by Andreas Fabri.