|
CGAL 6.1 - dD Triangulations
|
|
CGAL 6.1 - dD Triangulations
|
The TriangulationDataStructure concept describes objects responsible for storing and maintaining the combinatorial part of a \( d\)-dimensional pure simplicial complex that has the topology of the \( d\)-dimensional sphere \( \mathbb{S}^d\) with \( d\in[-2,D]\). Since the simplicial \( d\)-complex is pure, all faces are sub-faces of some \( d\)-simplex. And since it has the topology of the sphere \( \mathbb{S}^d\), it is manifold, thus any \( d-1\)-face belongs to exactly two \( d\)-dimensional full cells.
The concept TriangulationDataStructure includes two sub-concepts TriangulationDataStructure::Vertex and TriangulationDataStructure::FullCell.
Possible values for the current dimension \( d\) include
This corresponds to a single vertex and a single full cell, which is also the unique vertex and the unique full cell in the TriangulationDataStructure. In a geometric realization of the TriangulationDataStructure (e.g., in a Triangulation<TriangulationTraits_, TriangulationDataStructure_> or a Delaunay_triangulation<DelaunayTriangulationTraits_, TriangulationDataStructure_>), this vertex corresponds to the vertex at infinity.
This corresponds to two vertices, each incident to one \( 0\)-face; the two full cells being neighbors of each other. This is the unique triangulation of the \( 0\)-sphere.
An \( i\)-simplex is a simplex with \( i+1\) vertices. An \( i\)-simplex \( \sigma\) is incident to a \( j\)-simplex \( \sigma'\), \( j<i\), if and only if \( \sigma'\) is a proper face of \( \sigma\).
We call a \( 0\)-simplex a vertex, a \( (d-1)\)-simplex a facet and a \( d\)-simplex a full cell. A face can have any dimension. Two full cells are neighbors if they share a facet. Two faces are incident if one is included in the other.
Input/Output
The information stored in the iostream is:
tds.maximal_dimension()),The indices of vertices and full cells correspond to the order in the file; the user cannot control it. The classes Vertex and Full_cell have to provide the relevant I/O operators (possibly empty).
CGAL::Triangulation_data_structure<Dimensionality, TriangulationDSVertex_, TriangulationDSFullCell_> Concepts | |
| concept | FullCell |
The concept TriangulationDataStructure::FullCell describes the type used by a TriangulationDataStructure to store the full cells. More... | |
| concept | Vertex |
The concept TriangulationDataStructure::Vertex describes the type used by a TriangulationDataStructure to store the vertices. More... | |
Types | |
| typedef unspecified_type | Vertex |
The vertex type, requirements for this type are described in the concept TriangulationDataStructure::Vertex. | |
| typedef unspecified_type | Full_cell |
The full cell type, requirements for this type are described in the concept TriangulationDataStructure::FullCell. | |
| typedef unspecified_type | Full_cell_data |
A model of the concept FullCellData. | |
| typedef unspecified_type | Facet |
| The facet type, for describing faces of the triangulation with codimension 1. | |
| typedef unspecified_type | Face |
The face type, which must be a model of the concept TriangulationDSFace. | |
Handles | |
Vertices and full cells are manipulated via handles. Handles support the usual two dereference operators and | |
| typedef unspecified_type | Vertex_handle |
Handle to a Vertex. | |
| typedef unspecified_type | Vertex_const_handle |
Const handle to a Vertex. | |
| typedef unspecified_type | Full_cell_handle |
Handle to a Full_cell. | |
| typedef unspecified_type | Full_cell_const_handle |
Const handle to a Full_cell. | |
Iterators | |
Vertices, facets and full cells can be iterated over using iterators. Iterators support the usual two dereference operators and | |
| typedef unspecified_type | Vertex_iterator |
| Iterator over the list of vertices. | |
| typedef unspecified_type | Full_cell_iterator |
| Iterator over the list of full cells. | |
| typedef unspecified_type | Facet_iterator |
| Iterator over the facets of the complex. | |
| typedef unspecified_type | size_type |
| Size type (an unsigned integral type). | |
| typedef unspecified_type | difference_type |
| Difference type (a signed integral type). | |
Creation | |
| TriangulationDataStructure (int dim=0) | |
Creates an instance tds of type TriangulationDataStructure. | |
Queries | |
| int | maximal_dimension () const |
Returns the maximal dimension of the full dimensional cells that can be stored in the triangulation tds. | |
| int | current_dimension () const |
| Returns the dimension of the full dimensional cells stored in the triangulation. | |
| bool | empty () const |
Returns true if the triangulation contains nothing, returns false otherwise. | |
| size_type | number_of_vertices () const |
| Returns the number of vertices in the triangulation. | |
| size_type | number_of_full_cells () const |
| Returns the number of full cells in the triangulation. | |
| bool | is_vertex (const Vertex_handle &v) const |
Tests whether v is a vertex of the triangulation. | |
| bool | is_full_cell (const Full_cell_handle &c) const |
Tests whether c is a full cell of the triangulation. | |
| template<typename TraversalPredicate , typename OutputIterator > | |
| Facet | gather_full_cells (Full_cell_handle start, TraversalPredicate &tp, OutputIterator &out) const |
| This function computes (gathers) a connected set of full cells satisfying a common criterion. | |
| template<typename OutputIterator > | |
| OutputIterator | incident_full_cells (Vertex_handle v, OutputIterator out) const |
Inserts in out all the full cells that are incident to the vertex v, i.e., the full cells that have the Vertex v as a vertex. | |
| template<typename OutputIterator > | |
| OutputIterator | incident_full_cells (const Face &f, OutputIterator out) const |
Inserts in out all the full cells that are incident to the face f, i.e., the full cells that have the Face f as a subface. | |
| template<typename OutputIterator > | |
| OutputIterator | star (const Face &f, OutputIterator out) const |
Inserts in out all the full cells that share at least one vertex with the Face f. | |
| template<typename OutputIterator > | |
| OutputIterator | incident_faces (Vertex_handle v, const int dim, OutputIterator out) |
Constructs all the Faces of dimension dim incident to Vertex v and inserts them in the OutputIterator out. | |
Accessing the Vertices | |
| Vertex_handle | vertex (Full_cell_handle c, const int i) const |
Returns a handle to the i-th Vertex of the Full_cell c. | |
| int | mirror_index (Full_cell_handle c, int i) const |
Returns the index of c as a neighbor of its i-th neighbor. | |
| Vertex_handle | mirror_vertex (Full_cell_handle c, int i) const |
Returns the vertex of the i-th neighbor of c that is not vertex of c. | |
| Vertex_iterator | vertices_begin () |
Iterator to the first vertex of tds. | |
| Vertex_iterator | vertices_end () |
Iterator referring beyond the last vertex of tds. | |
Accessing the Full Cells | |
| Full_cell_handle | full_cell (Vertex_handle v) const |
Returns a full cell incident to Vertex v. | |
| Full_cell_handle | neighbor (Full_cell_handle c, int i) const |
Returns a Full_cell_handle pointing to the Full_cell opposite to the i-th vertex of c. | |
| Full_cell_iterator | full_cells_begin () |
Iterator to the first full cell of tds. | |
| Full_cell_iterator | full_cells_end () |
Iterator referring beyond the last full cell of tds. | |
Faces and Facets | |
| Facet_iterator | facets_begin () |
| Iterator to the first facet of the triangulation. | |
| Facet_iterator | facets_end () |
| Iterator referring beyond the last facet of the triangulation. | |
| Full_cell_handle | full_cell (const Facet &f) const |
Returns a full cell containing the facet f | |
| int | index_of_covertex (const Facet &f) const |
Returns the index of vertex of the full cell c=tds.full_cell(f) which does not belong to c. | |
Vertex Insertion | |
| Vertex_handle | insert_in_full_cell (Full_cell_handle c) |
Inserts a new vertex v in the full cell c and returns a handle to it. | |
| Vertex_handle | insert_in_face (const Face &f) |
Inserts a vertex in the triangulation data structure by subdividing the Face f. | |
| Vertex_handle | insert_in_facet (const Facet &ft) |
Inserts a vertex in the triangulation data structure by subdividing the Facet ft. | |
| template<class ForwardIterator > | |
| Vertex_handle | insert_in_hole (ForwardIterator start, ForwardIterator end, Facet f) |
| This is an advanced function. | |
| template<class ForwardIterator , class OutputIterator > | |
| Vertex_handle | insert_in_hole (ForwardIterator start, ForwardIterator end, Facet f, OutputIterator out) |
Same as above, but handles to the new full cells are appended to the out output iterator. | |
| Vertex_handle | insert_increase_dimension (Vertex_handle star) |
Transforms a triangulation of the sphere \( \mathbb{S}^d\) into the triangulation of the sphere \( \mathbb{S}^{d+1}\) by adding a new vertex v. | |
| Full_cell_handle | new_full_cell () |
Adds a new full cell to tds and returns a handle to it. | |
| Vertex_handle | new_vertex () |
Adds a new vertex to tds and returns a handle to it. | |
| void | associate_vertex_with_full_cell (Full_cell_handle c, int i, Vertex_handle v) |
Sets the i-th vertex of c to v and, if v != Vertex_handle(), sets c as the incident full cell of v. | |
| void | set_neighbors (Full_cell_handle ci, int i, Full_cell_handle cj, int j) |
Sets the neighbor opposite to vertex i of Full_cell ci to cj. | |
| void | set_current_dimension (int d) |
Forces the current dimension of the complex to d. | |
Vertex Removal | |
| void | clear () |
Reinitializes tds to the empty complex. | |
| Vertex_handle | collapse_face (const Face &f) |
Contracts the Face f to a single vertex. | |
| void | remove_decrease_dimension (Vertex_handle v, Vertex_handle star) |
This method does exactly the opposite of insert_increase_dimension(): v is removed, full cells not containing star are removed, full cells containing star but not v lose vertex star, full cells containing star and v lose vertex v (see Figure Figure 50.5). | |
| void | delete_vertex (Vertex_handle v) |
| This is an advanced function. | |
| void | delete_full_cell (Full_cell_handle c) |
| This is an advanced function. | |
| template<typename ForwardIterator > | |
| void | delete_full_cells (ForwardIterator start, ForwardIterator end) |
| This is an advanced function. | |
Validity Check | |
| bool | is_valid (bool verbose=false) const |
| This is a function for debugging purpose. | |
| std::istream & | operator>> (std::istream &is, TriangulationDataStructure &tds) |
Reads a combinatorial triangulation from is and assigns it to tds. | |
| std::ostream & | operator<< (std::ostream &os, const TriangulationDataStructure &tds) |
Writes tds into the output stream os. | |
The facet type, for describing faces of the triangulation with codimension 1.
The constructor Facet(c,i) constructs a Facet representing the facet of full cell c opposite to its i-th vertex. Its dimension is current_dimension()-1.
| TriangulationDataStructure::TriangulationDataStructure | ( | int | dim = 0 | ) |
Creates an instance tds of type TriangulationDataStructure.
The maximal dimension of its full cells is dim and tds is initialized to the empty triangulation. Thus, tds.current_dimension() equals -2. The parameter dim can be ignored by the constructor if it is already known at compile-time. Otherwise, the following precondition holds:
dim>0. | Vertex_handle TriangulationDataStructure::collapse_face | ( | const Face & | f | ) |
Contracts the Face f to a single vertex.
Returns a handle to that vertex (see Figure Figure 50.1).
f is a topological sphere of dimension tds.current_dimension()-1).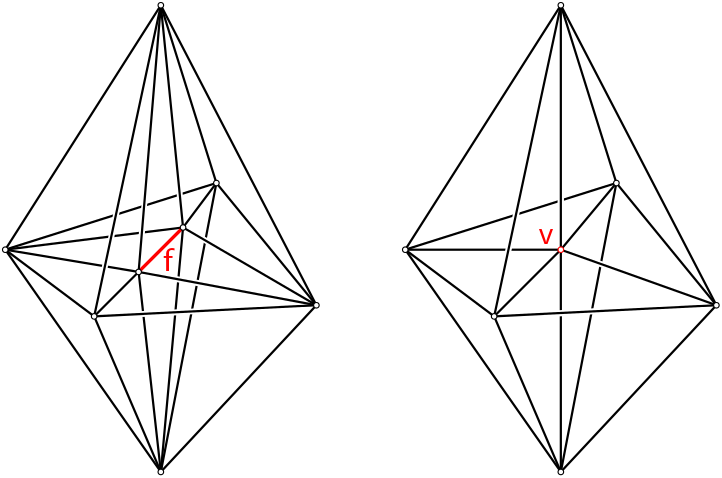
Figure 50.1 Collapsing an edge in dimension \( d=3\), v is returned.
| int TriangulationDataStructure::current_dimension | ( | ) | const |
Returns the dimension of the full dimensional cells stored in the triangulation.
It holds that tds.current_dimension()=-2 if and only if tds.empty() is true.
d satisfies \( -2\leq d \leq\)tds.maximal_dimension(). | void TriangulationDataStructure::delete_full_cell | ( | Full_cell_handle | c | ) |
This is an advanced function.
Remove the full cell c from the triangulation.
c is a full cell of tds. | void TriangulationDataStructure::delete_full_cells | ( | ForwardIterator | start, |
| ForwardIterator | end | ||
| ) |
This is an advanced function.
Calls delete_full_cell over an iterator range of value type Full_cell_handle.
| void TriangulationDataStructure::delete_vertex | ( | Vertex_handle | v | ) |
This is an advanced function.
Remove the vertex v from the triangulation.
v is a vertex of tds. | Full_cell_handle TriangulationDataStructure::full_cell | ( | Vertex_handle | v | ) | const |
Returns a full cell incident to Vertex v.
Note that this full cell is not unique (v is typically incident to more than one full cell).
v != Vertex_handle | Full_cell_iterator TriangulationDataStructure::full_cells_begin | ( | ) |
Iterator to the first full cell of tds.
User has no control on the order.
| Facet TriangulationDataStructure::gather_full_cells | ( | Full_cell_handle | start, |
| TraversalPredicate & | tp, | ||
| OutputIterator & | out | ||
| ) | const |
This function computes (gathers) a connected set of full cells satisfying a common criterion.
Call them good full cells. It is assumed that the argument start is a good full cell. The full cells are then recursively explored by examining if, from a given good full cell, its adjacent full cells are also good.
The argument tp is a predicate, i.e. a function or a functor providing operator(), that takes as argument a Facet whose Full_cell is good. The predicate must return true if the traversal of that Facet leads to a good full cell.
All the good full cells are output into the last argument out.
Returns a facet on the boundary of the set of cells.
start != Full_cell_handle() and start is a good cell. | OutputIterator TriangulationDataStructure::incident_faces | ( | Vertex_handle | v, |
| const int | dim, | ||
| OutputIterator | out | ||
| ) |
Constructs all the Faces of dimension dim incident to Vertex v and inserts them in the OutputIterator out.
If dim >= tds.current_dimension(), then no Face is constructed.
0 < dim and v!=Vertex_handle(). | OutputIterator TriangulationDataStructure::incident_full_cells | ( | const Face & | f, |
| OutputIterator | out | ||
| ) | const |
Inserts in out all the full cells that are incident to the face f, i.e., the full cells that have the Face f as a subface.
Returns the output iterator.
f.full_cell()!=Full_cell_handle(). | OutputIterator TriangulationDataStructure::incident_full_cells | ( | Vertex_handle | v, |
| OutputIterator | out | ||
| ) | const |
Inserts in out all the full cells that are incident to the vertex v, i.e., the full cells that have the Vertex v as a vertex.
Returns the output iterator.
v!=Vertex_handle(). | Vertex_handle TriangulationDataStructure::insert_in_face | ( | const Face & | f | ) |
Inserts a vertex in the triangulation data structure by subdividing the Face f.
Returns a handle to the newly created Vertex.
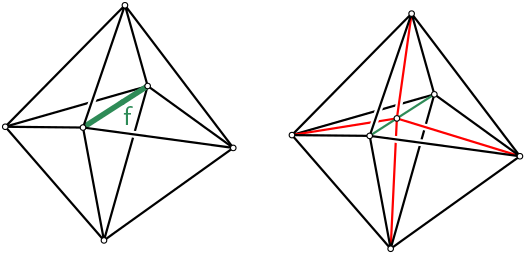
Figure 50.2 Insertion in face, \( d=3\)
| Vertex_handle TriangulationDataStructure::insert_in_facet | ( | const Facet & | ft | ) |
Inserts a vertex in the triangulation data structure by subdividing the Facet ft.
Returns a handle to the newly created Vertex.
| Vertex_handle TriangulationDataStructure::insert_in_full_cell | ( | Full_cell_handle | c | ) |
Inserts a new vertex v in the full cell c and returns a handle to it.
The full cell c is subdivided into tds.current_dimension()+1 full cells which share the vertex v.
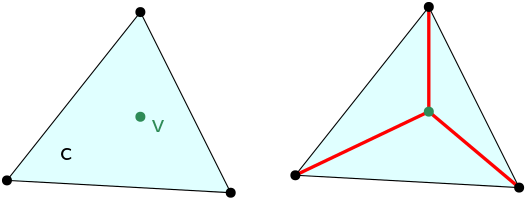
Figure 50.3 Insertion in a full cell, \( d=2\)
c is a full cell of tds. | Vertex_handle TriangulationDataStructure::insert_in_hole | ( | ForwardIterator | start, |
| ForwardIterator | end, | ||
| Facet | f | ||
| ) |
This is an advanced function.
Removes the full cells in the range \( C=\)[s, e), inserts a vertex at position p and fills the hole by connecting each face of the boundary to p. A Vertex_handle to the new Vertex is returned. The facet ft must lie on the boundary of \( C\) and its defining full cell, tr.full_cell(ft) must lie inside \( C\). Handles to the newly created full cells are output in the out output iterator.
c belongs to \( C\) and c->neighbor(i) does not, with f=(c,i). \( H\), the union of full cells in \( C\), is simply connected and its boundary \( \partial H\) is a combinatorial triangulation of the sphere \( \mathbb{S}^{d-1}\). All vertices of cells of \( C\) are on \( \partial H\).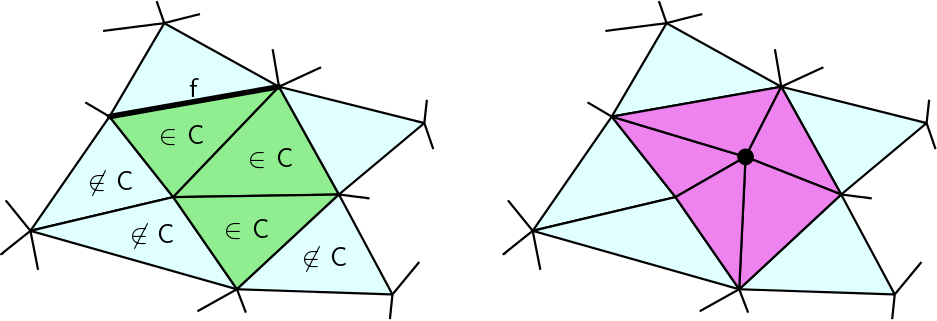
Figure 50.4 Insertion in a hole, \( d=2\)
| Vertex_handle TriangulationDataStructure::insert_increase_dimension | ( | Vertex_handle | star | ) |
Transforms a triangulation of the sphere \( \mathbb{S}^d\) into the triangulation of the sphere \( \mathbb{S}^{d+1}\) by adding a new vertex v.
v is used to triangulate one of the two half-spheres of \( \mathbb{S}^{d+1}\) ( \( v\) is added as \( (d+2)^{th}\) vertex to all full cells) and star is used to triangulate the other half-sphere (all full cells that do not already have star as vertex are duplicated, and star replaces v in these full cells). The indexing of the vertices in the full cell is such that, if f was a full cell of maximal dimension in the initial complex, then (f,v), in this order, is the corresponding full cell in the updated triangulation. A handle to v is returned (see Figure Figure 50.5).
star can be omitted (it is ignored), otherwise the current dimension must be strictly less than the maximal dimension and star must be a vertex of tds.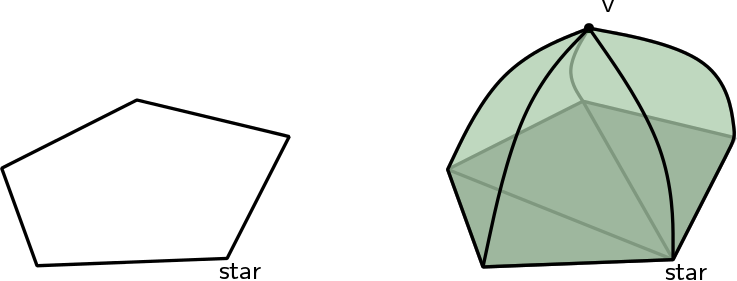
Figure 50.5 Insertion, increasing the dimension from \( d=1\) to \( d=2\)
| bool TriangulationDataStructure::is_valid | ( | bool | verbose = false | ) | const |
This is a function for debugging purpose.
Partially checks whether tds is indeed a triangulation.
It must at least
tds by calling their respective is_valid method. current_dimension()+1). tds.current_dimension() vertices with each of its neighbor. When verbose is set to true, messages are printed to give a precise indication on the kind of invalidity encountered.
Returns true if all the tests pass, false if any test fails. See the documentation for the models of this concept to see the additional (if any) validity checks that they implement.
| int TriangulationDataStructure::maximal_dimension | ( | ) | const |
Returns the maximal dimension of the full dimensional cells that can be stored in the triangulation tds.
| int TriangulationDataStructure::mirror_index | ( | Full_cell_handle | c, |
| int | i | ||
| ) | const |
Returns the index of c as a neighbor of its i-th neighbor.
tds.current_dimension() and c!=Full_cell_handle(). | Vertex_handle TriangulationDataStructure::mirror_vertex | ( | Full_cell_handle | c, |
| int | i | ||
| ) | const |
Returns the vertex of the i-th neighbor of c that is not vertex of c.
tds.current_dimension() and c!=Full_cell_handle(). | Full_cell_handle TriangulationDataStructure::neighbor | ( | Full_cell_handle | c, |
| int | i | ||
| ) | const |
Returns a Full_cell_handle pointing to the Full_cell opposite to the i-th vertex of c.
tds.current_dimension() and c != Full_cell_handle() | Full_cell_handle TriangulationDataStructure::new_full_cell | ( | ) |
Adds a new full cell to tds and returns a handle to it.
The new full cell has no vertices and no neighbors yet.
| Vertex_handle TriangulationDataStructure::new_vertex | ( | ) |
Adds a new vertex to tds and returns a handle to it.
The new vertex has no associated full cell nor index yet.
| std::istream & TriangulationDataStructure::operator>> | ( | std::istream & | is, |
| TriangulationDataStructure & | tds | ||
| ) |
Reads a combinatorial triangulation from is and assigns it to tds.
tds.maximal_dimension(). | void TriangulationDataStructure::remove_decrease_dimension | ( | Vertex_handle | v, |
| Vertex_handle | star | ||
| ) |
This method does exactly the opposite of insert_increase_dimension(): v is removed, full cells not containing star are removed, full cells containing star but not v lose vertex star, full cells containing star and v lose vertex v (see Figure Figure 50.5).
star or v. Edge star-v exists in the triangulation and current_dimension() != -2. | void TriangulationDataStructure::set_current_dimension | ( | int | d | ) |
Forces the current dimension of the complex to d.
maximal_dimension(). | void TriangulationDataStructure::set_neighbors | ( | Full_cell_handle | ci, |
| int | i, | ||
| Full_cell_handle | cj, | ||
| int | j | ||
| ) |
Sets the neighbor opposite to vertex i of Full_cell ci to cj.
Sets the neighbor opposite to vertex j of Full_cell cj to ci.
| OutputIterator TriangulationDataStructure::star | ( | const Face & | f, |
| OutputIterator | out | ||
| ) | const |
Inserts in out all the full cells that share at least one vertex with the Face f.
Returns the output iterator.
f.full_cell()!=Full_cell_handle(). | Vertex_handle TriangulationDataStructure::vertex | ( | Full_cell_handle | c, |
| const int | i | ||
| ) | const |
Returns a handle to the i-th Vertex of the Full_cell c.
tds.current_dimension() and c!=Full_cell_handle(). | Vertex_iterator TriangulationDataStructure::vertices_begin | ( | ) |
Iterator to the first vertex of tds.
User has no control on the order.