Author: Amal Dev Parakkat, Stefan Ohrhallinger, Elmar Eisemann, Pooran Memari

This CGAL component implements a surface reconstruction method that takes an unoriented set of 3D points as input and computes a piece-wise linear approximation of the sampled surface. In simple words, the method tries to classify the medial balls (computed from the 3D Delaunay triangulation of the input points) into interior and exterior and returns the interface between them.

The detailed description of the algorithm can be seen in [2].

1 Definitions

The method is built upon the fact that whenever a discrete set of sample points approximates a continuous surface, the Voronoi balls (interior/exterior) intersect along the boundary with a ratio inversely proportional to the sampling density (similar to the observation of Amenta et al. [1]). Based on this, we define an "intersection ratio" between adjacent Voronoi balls as follows:

$ir(B_0,B_1) = max((r_0+r_1-d)/r_0,(r_0+r_1-d)/r_1)$

Where $B_0$ and $B_1$ are two adjacent Voronoi balls with radius $r_0$ and $r_1$ respectively, and $d$ is the distance between it's circumcenters.

Using this ratio, we can say that if the intersection ratio between two adjacent Voronoi balls is small, they likely correspond to a pair of interior and exterior balls sharing a thin overlapping region along the underlying surface (a 2D case is illustrated in Figure Figure 67.1). In other words, given a threshold $\delta$ , a triangle is said to belong to a set $BallMerge(\delta)$ if its corresponding adjacent Voronoi balls have an intersection ratio less than $\delta$ . By definition, $BallMerge(\delta)$ is a subcomplex of the Delaunay Triangulation of the sample points. It is easy to see that $BallMerge(0)$ is empty, while $BallMerge(\delta)$ , for any $\delta \gt 2$ contains all the triangles of the Delaunay Triangulation.

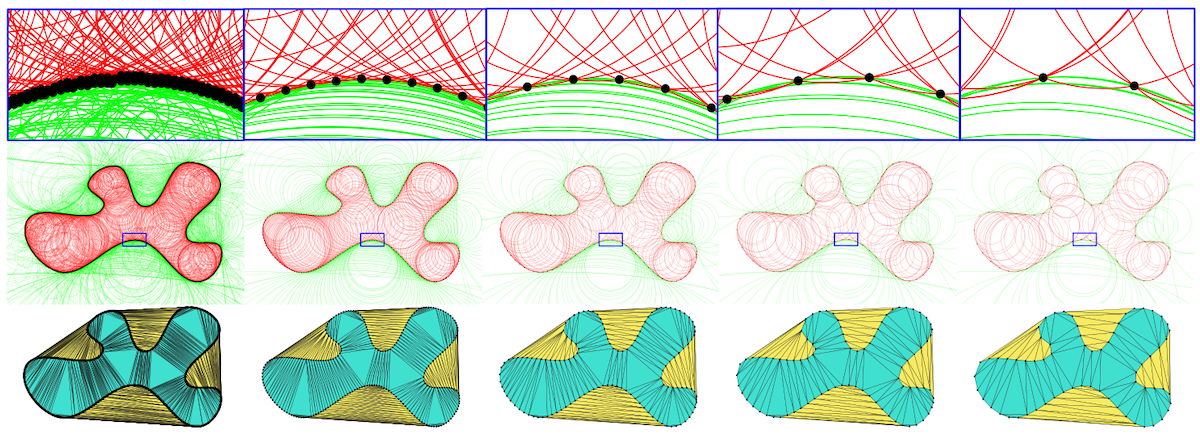
Figure 67.1 Top: The interior (red) and exterior (green) medial balls of a point set with decreasing point density from l.t.r. Bottom: Corresponding $\delta$ -merged components on Delaunay triangulation.

CGAL provides two variants of BallMerge:

Global BallMerge (ball_merge_surface_reconstruction_global()): Given a threshold $\delta$ , two Delaunay simplices are called $\delta$ -merged either if their corresponding Voronoi balls are adjacent with an intersection ratio $> \delta$ or if there exists another Delaunay simplex, which is $\delta$ -merged with both of them. Following a procedure similar to classical connected component computation, the algorithm starts by visiting $\delta$ -merged simplices from an arbitrary seed simplex (the procedure is order independent) and tag them with the current component label until no more $\delta$ -merged simplices remain. The procedure is then restarted with any yet unvisited simplex until all have been visited, and output the simplices with the most frequent label. The reconstructed surface is then computed from the boundary of this output. Local BallMerge (ball_merge_surface_reconstruction_local()): In this variant, for any two adjacent $d$ -simplices, which are not $\delta$ -mergeable, the shared $(d − 1)$ -simplex is retained. As outliers and open surfaces typically result in large simplices, we keep an additional constraint that makes two elements $\delta$ -mergeable only if the longest edge of the simplex is smaller than $\frac{1}{\eta}*\beta$ ( $\eta$ is a scaling factor, $\beta$ is the length of the bounding box diagonal) aiming at removing large simplices.

1.1 Choosing between Global and Local Variants

The Global variant, by definition, results in a watertight surface (not always manifold) and, hence, is optimal for reconstructing closed surfaces. As the algorithm tries to close the surface, it can withstand missing data up to an extent and can handle little outliers and noise.

The Local variant, however, is designed for handling open surfaces. As it is lightweight and requires only a single pass over the Delaunay simplices, it is optimal for reconstruction from an extremely huge point cloud.

1.2 Parameter Settings

The main parameter used in BallMerge is the intersection ratio $> \delta$ . By definition, the $> \delta$ ranges from 0 to 2 - with $BallMerge(0)$ being empty and $BallMerge(2)$ containing all the triangles of the Delaunay Triangulation. Experiments show that the $> \delta$ value usually lies between 1.5 and 1.95 (with 1.8 or 1.85 giving the best results in most cases). Thanks to the nice property of this intersection ratio, it is quite easy to tune this parameter based on a simple rule: if the reconstructed surface has missing parts, the threshold should be lowered, or if the reconstructed surface has additional parts, the threshold should be increased. The objective of the other parameter $\eta$ is to remove unnecessarily long triangles from the result of Local BallMerge. In practice, the threshold $\eta = 200$ was observed to perform well and can be adjusted - Figure Figure 67.2 shows the effect of varying $\eta$ .

Figure 67.2 Effect of $\eta$ ( $\delta$ = 1.8); l.t.r.: $\eta$ = 5,50,100,150,200,250,300 (original mesh taken from EPFL Statue Repository).

2 Examples

Two functions ball_merge_surface_reconstruction_global() and ball_merge_surface_reconstruction_local() are provided to use $GlobalBallMerge$ and $LocalBallMerge$ functionalities.

ball_merge_surface_reconstruction_global() has the following arguments: The set of input points, two output parameters where the resulting meshes will be stored, and the parameter $\delta$ . The function returns two meshes - the largest and second-largest components as sometimes the expected shape will be the second-largest component after merging. A sample program showing how to use this function is given below:

File Ball_merge_surface_reconstruction/ball_merge_reconstruction_global.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Ball_merge_surface_reconstruction.h>
#include <CGAL/IO/polygon_soup_io.h>
#include <CGAL/IO/read_points.h>
 
#include <string>
 
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_3 Point;
 
namespace params=CGAL::parameters;
 
int main(int argc, char **argv)
{
  // reading input points and parameters
  const std::string inFilename=argc>1?argv[1]:CGAL::data_file_path("points_3/kitten.xyz");
  double delta = argc>2?atof(argv[2]):1.7;
  std::vector<Point> points;
  CGAL::IO::read_points(inFilename, std::back_inserter(points));
 
  if (points.empty())
  {
    std::cerr << inFilename << " cannot be read correctly or is empty.\n";
    return 1;
  }
 
  //vectors for storing output triangle indices
  std::vector<std::array<int,3>> meshFaceIndices1, meshFaceIndices2;
 
  // run the reconstruction with the given parameter
  CGAL::ball_merge_surface_reconstruction_global(
    points,
    meshFaceIndices1, meshFaceIndices2,
    params::delta(delta).concurrency_tag(CGAL::Parallel_if_available_tag()));
 
  // write output triangle soups
  CGAL::IO::write_polygon_soup("BMOut1.ply", points, meshFaceIndices1); //The first resulting mesh
  CGAL::IO::write_polygon_soup("BMOut2.ply", points, meshFaceIndices2); //The second resulting mesh
 
  return 0;
}

ball_merge_surface_reconstruction_local() has the following arguments: The set of input points, an output parameter where the resulting mesh will be stored, the parameter $\delta$ , and the parameter $\eta$ (to prune unnecessary long triangles). A sample program showing how to use this function is given below:

File Ball_merge_surface_reconstruction/ball_merge_reconstruction_local.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Ball_merge_surface_reconstruction.h>
#include <CGAL/IO/polygon_soup_io.h>
#include <CGAL/IO/read_points.h>
 
#include <string>
 
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_3 Point;
 
namespace params=CGAL::parameters;
 
int main(int argc, char **argv)
{
  // reading input points and parameters
  std::string inFilename=argc>1?argv[1]:CGAL::data_file_path("points_3/hippo2.ply"); //Test input file
  double delta = argc>2?atof(argv[2]):1.8;
  double eta= argc>3?atof(argv[3]):40.;
  std::vector<Point> points;
  CGAL::IO::read_points(inFilename, std::back_inserter(points)); //Reading the input points
 
  if (points.empty())
  {
    std::cerr << inFilename << " cannot be read correctly or is empty.\n";
    return 1;
  }
 
  //vector for storing output triangle indices
  std::vector<std::array<int,3>> meshFaceIndices;
 
  // run the reconstruction with the given parameters
  CGAL::ball_merge_surface_reconstruction_local(
    points, meshFaceIndices, params::delta(delta)
                                    .eta(eta)
                                    .concurrency_tag(CGAL::Parallel_if_available_tag()));
 
  // write output triangle soups
  CGAL::IO::write_polygon_soup("BMOut1.ply", points, meshFaceIndices);
 
  return 0;
}

Alternatively, these functions can be combined as in the following program where argv[1] is the filename, argv[2] is the parameter $\delta$ , argv[3] decides whether to use local (0) or global variant (1), and arg[4] is an optional parameter $\eta$ in case the user opts for the local variant.

File Ball_merge_surface_reconstruction/ball_merge_reconstruction.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Ball_merge_surface_reconstruction.h>
#include <CGAL/IO/polygon_soup_io.h>
#include <CGAL/IO/read_points.h>
 
#include <string>
 
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef K::Point_3 Point;
 
namespace params=CGAL::parameters;
 
int main(int argc, char **argv)
{
  // reading input points and parameters
  std::string inFilename = argc>1?argv[1]:CGAL::data_file_path("points_3/kitten.xyz");//Filename
  double delta = argc>2?atof(argv[2]):1.7;
 
  //Select to select between global and local variants 0 for local and any other value for global
  int option = argc>3?atoi(argv[3]):1;
 
  std::vector<Point> points;
  CGAL::IO::read_points(inFilename, std::back_inserter(points));
 
  if (points.empty())
  {
    std::cerr << inFilename << " cannot be read correctly or is empty.\n";
    return 1;
  }
 
  if (option == 0)
  {
    // reading an extra parameter
    double eta = (argc >= 5) ? atof(argv[4]) : 200.;
 
    //vector for storing output triangle indices
    std::vector<std::array<int,3>> meshFaceIndices;
 
    // run the reconstruction with the given parameters
    CGAL::ball_merge_surface_reconstruction_local(
      points, meshFaceIndices,
      params::delta(delta).eta(eta).concurrency_tag(CGAL::Parallel_if_available_tag()));
 
    // write output triangle soup
    CGAL::IO::write_polygon_soup("BMOut1.ply", points, meshFaceIndices);
  }
  else{
    //vectors for storing output triangle indices
    std::vector<std::array<int,3>> meshFaceIndices1, meshFaceIndices2;
 
    // run the reconstruction with the given parameter
    CGAL::ball_merge_surface_reconstruction_global(
      points, meshFaceIndices1, meshFaceIndices2,
      params::delta(delta).concurrency_tag(CGAL::Parallel_if_available_tag()));
 
    // write output triangle soups
    CGAL::IO::write_polygon_soup("BMOut1.ply", points, meshFaceIndices1);
    CGAL::IO::write_polygon_soup("BMOut2.ply", points, meshFaceIndices2);
  }
 
  return 0;
}

Ideally, the current implementation takes a dense point cloud as input (plain x,y,z coordinates without any additional information like normal and texture) sampled over a smooth surface. Thanks to the "intersection ratio", the algorithm can also handle a few challenging cases with mild noise, outliers or missing data up to an extent. It is worth noting that, while using $GlobalBallMerge$ , outliers sometimes create deep cavities over the surface, and an increased amount of noise shrinks and sometimes misses important features.

Finally, the algorithm is lightweight and requires only a little computation in terms of input size as it performs only two quick linear-time passes on the Delaunay complex (global) or just a single pass (local).

3 Implementation History

This package is based on a prototype code .....