User Manual

Author

Mael Rouxel-Labbé, Julian Stahl, Daniel Zint, and Pierre Alliez

Figure 61.1 Generating a surface from a 3D gray level image using Marching Cubes (3D input image: qim.dk)

Introduction

Given a field of a scalar values, an isosurface is defined as the locus of points where the field has a given constant value; in other words, it is a level set. This constant value is referred to as the "isovalue", and, for well-behaved fields, the level set forms a surface. In the following, we shall refer to the the field of scalar values as the value field. "Isosurfacing", also known as "isosurface extraction" or "contouring", is the process of constructing the isosurface corresponding to a given value field and isovalue. Isosurfacing is often needed for volume visualization and for the simulation of physical phenomena.

This CGAL package provides methods to extract isosurfaces from 3D value fields. These contouring techniques rely on the partition of the 3D space and of the field to construct an approximate representation of the isosurface. The 3D value field can be described through various representations: an implicit function, an interpolated set of discrete sampling values, etc. (see Examples). The isovalue is user-defined. The output is a polygon soup, made either of triangles or quads depending on the method, and may consist of a single connected component, or multiple, disjoint components. Note that due to the inherent approximate nature of these discrete methods that only sample 3D value fields, parts of the "true" isosurface may be missing from the output, and the output may contain artifacts that re not present in the true isosurface.

Isosurfacing Methods

The scientific literature abounds with algorithms for extracting isosurfaces, each coming with different properties for the output and requirements for the input [2]. This package offers the following methods

• Marching Cubes (MC) : a simple and efficient method that generates a triangle mesh, with almost no guarantees.
• Topologically Correct Marching Cubes (TMC) : an extension to Marching Cubes that provides additional guarantees for the output.
• Dual Contouring (DC) : a method that generates a polygon mesh, with a focus on sharp features recovery.

Marching Cubes (MC)

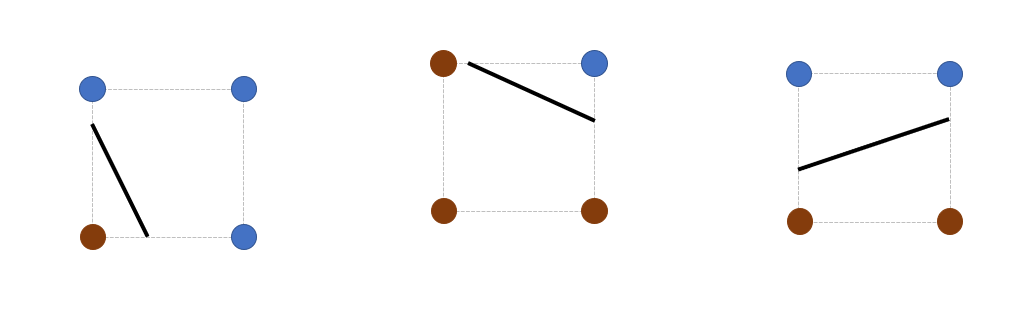
Marching Cubes (MC) [5] uses a volumetric grid, i.e., a 3D iso-cuboid partitioned into hexahedral cells. All cells of the grid are processed individually using values of the value field sampled at the grid corners. Each cell corner is assigned a sign (+/-) to indicate whether its value field value is above or below the user-defined isovalue. A vertex is created along each grid edge where a sign change occurs, i.e., where the edge intersects the isosurface. More specifically, the vertex location is computed via linear interpolation of the value field values evaluated at the cell corners forming the edge. These vertices are connected to form triangles within the cell, depending on the configuration of signs at the cell corners. Figure 61.2 illustrates the configurations in 2D. In 3D, there are no less than 33 configurations (not shown) [1].

Figure 61.2 Examples of some configurations for 2D Marching Cubes.

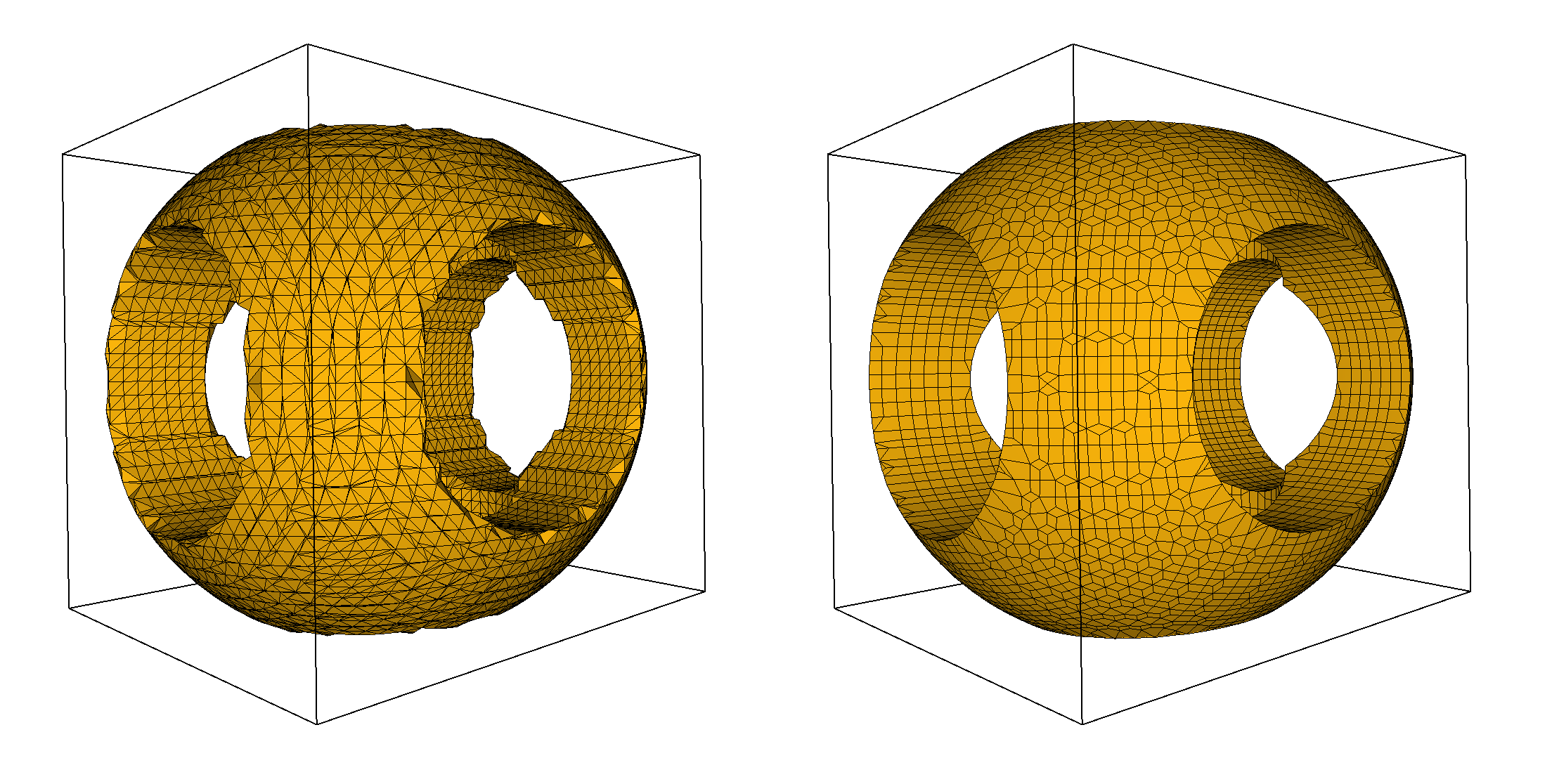
The implementation within CGAL is generic in the sense that it can process any grid-like data structure that consists of hexahedral cells. When the hexahedral grid is a conforming grid (meaning that the intersection of two hexahedral cells is a face, an edge, or a vertex), the Marching Cubes algorithm generates as output a surface triangle mesh that is almost always combinatorially 2-manifold, yet can still exhibit topological issues such as holes or non-conforming edges.

If the mesh is 2-manifold and the isosurface does not intersect the domain boundary, then the output mesh is watertight. As the Marching Cubes algorithm uses linear interpolation of the sampled value field along the grid edges, it can miss details or components that are not captured by the sampling of the value field.

Compared to other meshing approaches such as Delaunay refinement, Marching Cubes is substantially faster, but often tends to generate more triangle facets for an equivalent desired sizing field. In addition, the quality of the triangle facets is in general poor, with many needle/cap shaped triangles.

Furthermore, Marching Cubes does not preserve the sharp features present in the isovalue of the input value field (see Figure 61.4).

Topologically Correct Marching Cubes (TMC)

Topologically Correct Marching Cubes is an extension to the Marching Cubes algorithm which provides additional guarantees for the output [3]. More specifically, it generates as output a mesh that is homeomorphic to the trilinear interpolant of the input value field inside each cube. This means that the output mesh can accurately represent small complex features. For example, a tunnel of the isosurface within a single cell is topologically resolved. To achieve this, the algorithm can insert additional vertices within cells. Furthermore, the mesh is guaranteed to be 2-manifold and watertight, as long as the isosurface does not intersect the domain boundaries.

Figure 61.3 Marching Cubes vs Topologically Correct Marching Cubes.

Dual Contouring (DC)

Dual Contouring (DC) [4] is a method that does not generate vertices on the grid edges, but within cells instead. A facet is created for each edge that intersects the isosurface by connecting the vertices of the incident cells. For a uniform hexahedral grid, this results in a quadrilateral surface mesh. Dual Contouring can deal with any domain but guarantees neither a 2-manifold nor a watertight mesh. On the other hand, it generates fewer faces and higher quality faces than Marching Cubes, in general. Finally, its main advantage over Marching Cubes is its ability to recover sharp creases and corners.

Figure 61.4 Comparison between a mesh of a CSG shape generated by Marching Cubes (left) and Dual Contouring (right).

In addition to the 3D value field, Dual Contouring requires knowledge about the gradient of the value field.

The CGAL implementation uses a vertex positioning strategy based on Quadric Error Metrics: for a cell, the vertex location is computed by minimizing the error to the sum of the quadrics defined at each edge-isosurface intersection. Using this approach, the vertex may be located outside the cell, which is a desirable property to improve the odds of recovering sharp features, but it might also create self-intersections. Users can choose to constrain the vertex location inside the cell.

By default, Dual Contouring generates quads, but using edge-isosurface intersections, one can "star" these quads to generate four triangles. Triangulating the quads is the default behavior in CGAL, but this can be changed via named parameters.

Comparisons

The following table summarizes the differences between the algorithms in terms of constraints over the input 3D domain, the facets of the output surface mesh, and the properties of the output surface mesh.

Algorithm	Facets	2-Manifold	Watertight*	Topologically correct	Recovery of Sharp Features
MC	Triangles	no	no	no	no
TMC	Triangles	yes	yes	yes	no
DC	Polygons	no	no	no	yes (not guaranteed)

(* assuming the isosurface does not exit the specified bounding box of the input 3D domain)

Note that the output mesh has boundaries when the isosurface intersects the domain boundaries, regardless of the method (see Figure 61.5).

Figure 61.5 Outputs of Marching Cubes (left) and Dual Contouring (right) for an implicit sphere of radius 1.1 and a domain of size 2x2x2, both centered at the origin. Output meshes can have boundaries when the isosurface intersects the domain boundary.

Interface

The following functions are the main entry points to the isosurfacing algorithms:

• Marching Cubes: CGAL::Isosurfacing::marching_cubes(), using the named parameter:use_topologically_correct_marching_cubes set to false;
• Topologically Correct Marching Cubes: CGAL::Isosurfacing::marching_cubes();
• Dual Contouring: CGAL::Isosurfacing::dual_contouring().

These three free functions share the same signature:

template <typename ConcurrencyTag = CGAL::Sequential_tag,
          typename Domain,
          typename PointRange,
          typename PolygonRange>
void ...(const Domain& domain,
         const typename Domain::FT isovalue,
         PointRange& points,
         PolygonRange& polygons);

The input (space partition, value field, gradient field) is provided in the form of a domain, see Domains for a complete description.

The isovalue scalar parameter is the value that defines the isosurface being approximated.

The output discrete surface is provided in the form of a polygon soup, which is stored into two containers: points and polygons. Depending on the algorithm, the polygon soup may store either unorganized polygons with no relationship to one another (ie, no connectivity is shared between them) or polygons sharing points (the same point in adjacent polygons will be the same point in the point range).

The isosurfacing algorithms can run either sequentially in one thread or in parallel via multithreading. The template parameter ConcurrencyTag is used to specify how the algorithm is executed. To enable parallelism, CGAL must be linked with the Intel TBB library (see the CMakeLists.txt file in the examples folder).

Domains

A domain is an object that provides functions to access the partition of the 3D volume, the value field, and, optionally, the gradient field at a given point query. These requirements are described through two concepts: IsosurfacingDomain_3 and IsosurfacingDomainWithGradient_3.

Two domains, CGAL::Isosurfacing::Marching_cubes_domain_3 and CGAL::Isosurfacing::Dual_contouring_domain_3, are provided as the respective default class models that fulfill the requirements of the concepts. Both these domain models have template parameters enabling the user to customize the domain:

• Partition: this must be a class that describes the partition of the 3D volume into cells. The most basic example of such a class is CGAL::Isosurfacing::Cartesian_grid_3, but users can pass their own partition, provided it meets the requirements described by the concept IsosurfacingPartition_3.
• ValueField: this must be a class that provides the 3D value field at the vertices of the partition. A few classes are provided, such as CGAL::Isosurfacing::Value_function_3 and CGAL::Isosurfacing::Interpolated_discrete_values_3. Users can pass their own value class, provided it meets the requirements described by the concept IsosurfacingValueField_3.
• GradientField: (CGAL::Isosurfacing::Dual_contouring_domain_3 only) this must be a class that provides the gradient of the value field at the vertices of the partition. A few classes are provided by default, such as CGAL::Isosurfacing::Finite_difference_gradient_3 and CGAL::Isosurfacing::Interpolated_discrete_gradients_3. Users can pass their own gradient class, provided it meets the requirements described by the concept IsosurfacingGradientField_3.
• EdgeIntersectionOracle: this must be a class that provides a function to compute the intersection between an edge and the isosurface. The default is linear interpolation for CGAL::Isosurfacing::Marching_cubes_domain_3, and a dichotomy for CGAL::Isosurfacing::Dual_contouring_domain_3. This parameter should be adjusted depending on how the value field is defined: there is for example no point incorporating a dichotomy in Dual Contouring if the value field is defined through linear interpolation. Users can pass their own edge intersection oracle, provided it meets the requirements described by the concept IsosurfacingEdgeIntersectionOracle_3.

Performance

Due to their cell-based nature, the isosurfacing algorithms are well-suited for parallel execution.

Examples

The first two examples are very basic examples for Marching Cubes and Dual Contouring. Afterwards, the focus is shifted from the method to the type of input data, and examples run both methods on different types of input data.

Marching Cubes

The following example illustrates a basic run of the Marching Cubes algorithm, and in particular the free function to create a domain from a Cartesian grid, and the named parameter that enables the user to switch from Marching Cubes to Topologically Correct Marching Cubes.

File Isosurfacing_3/marching_cubes.cpp

#include <CGAL/Simple_cartesian.h>
 
#include <CGAL/Isosurfacing_3/Cartesian_grid_3.h>
#include <CGAL/Isosurfacing_3/Value_function_3.h>
#include <CGAL/Isosurfacing_3/marching_cubes_3.h>
#include <CGAL/Isosurfacing_3/Marching_cubes_domain_3.h>
 
#include <CGAL/IO/polygon_soup_io.h>
 
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Point = typename Kernel::Point_3;
using Vector = typename Kernel::Vector_3;
 
using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel>;
using Values = CGAL::Isosurfacing::Value_function_3<Grid>;
using Domain = CGAL::Isosurfacing::Marching_cubes_domain_3<Grid, Values>;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
int main(int argc, char** argv)
{
  const FT isovalue = (argc > 1) ? std::stod(argv[1]) : 0.8;
 
  // create bounding box and grid
  const CGAL::Bbox_3 bbox { -1., -1., -1., 1., 1., 1. };
  Grid grid { bbox, CGAL::make_array<std::size_t>(30, 30, 30) };
 
  std::cout << "Span: " << grid.span() << std::endl;
  std::cout << "Cell dimensions: " << grid.spacing()[0] << " " << grid.spacing()[1] << " " << grid.spacing()[2] << std::endl;
  std::cout << "Cell #: " << grid.xdim() << ", " << grid.ydim() << ", " << grid.zdim() << std::endl;
 
  // fill up values
  auto sphere_value_fn = [](const Point& p) -> FT
  {
    return sqrt(p.x()*p.x() + p.y()*p.y() + p.z()*p.z());
  };
 
  Values values { sphere_value_fn, grid };
 
  // Below is equivalent to:
  //   Domain domain { grid, values };
  Domain domain = CGAL::Isosurfacing::create_marching_cubes_domain_3(grid, values);
 
  Point_range points;
  Polygon_range triangles;
 
  // run marching cubes isosurfacing
  std::cout << "Running Marching Cubes with isovalue = " << isovalue << std::endl;
  CGAL::Isosurfacing::marching_cubes<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles,
                                                                      CGAL::parameters::use_topologically_correct_marching_cubes(true));
 
  std::cout << "Output #vertices: " << points.size() << std::endl;
  std::cout << "Output #triangles: " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("marching_cubes.off", points, triangles);
 
  std::cout << "Done" << std::endl;
 
  return EXIT_SUCCESS;
}

Dual Contouring

The following example illustrates a basic run of the Dual Contouring algorithm, and in particular the free function to create a domain from a Cartesian grid, and the named parameters that enable (or disable) triangulation of the output, and to constrain the vertex location within the cell.

File Isosurfacing_3/dual_contouring.cpp

#include <CGAL/Simple_cartesian.h>
 
#include <CGAL/Isosurfacing_3/Cartesian_grid_3.h>
#include <CGAL/Isosurfacing_3/dual_contouring_3.h>
#include <CGAL/Isosurfacing_3/Dual_contouring_domain_3.h>
#include <CGAL/Isosurfacing_3/Value_function_3.h>
#include <CGAL/Isosurfacing_3/Gradient_function_3.h>
 
#include <CGAL/IO/polygon_soup_io.h>
 
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Point = typename Kernel::Point_3;
using Vector = typename Kernel::Vector_3;
 
using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel>;
using Values = CGAL::Isosurfacing::Value_function_3<Grid>;
using Gradients = CGAL::Isosurfacing::Gradient_function_3<Grid>;
using Domain = CGAL::Isosurfacing::Dual_contouring_domain_3<Grid, Values, Gradients>;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
// https://www-sop.inria.fr/galaad/surface/
auto devil_value = [](const Point& point)
{
  const FT x = point.x(), y = point.y(), z = point.z();
  return x*x*x*x + 2*x*x*z*z - 0.36*x*x - y*y*y*y + 0.25*y*y + z*z*z*z;
};
 
auto devil_gradient = [](const Point& point)
{
  const FT x = point.x(), y = point.y(), z = point.z();
 
  const FT gx = 4*x*x*x + 4*x*z*z - 0.72*x;
  const FT gy = -4*y*y*y + 0.5*y;
  const FT gz = 4*x*x*z + 4*z*z*z;
  Vector g(gx, gy, gz);
  return g / std::sqrt(gx*gx + gy*gy + gz*gz);
};
 
int main(int argc, char** argv)
{
  const FT isovalue = (argc > 1) ? std::stod(argv[1]) : 0.;
 
  // create bounding box and grid
  const CGAL::Bbox_3 bbox { -1, -1, -1, 1, 1, 1 };
  Grid grid { bbox, CGAL::make_array<std::size_t>(50, 50, 50) };
 
  std::cout << "Span: " << grid.span() << std::endl;
  std::cout << "Cell dimensions: " << grid.spacing()[0] << " " << grid.spacing()[1] << " " << grid.spacing()[2] << std::endl;
  std::cout << "Cell #: " << grid.xdim() << ", " << grid.ydim() << ", " << grid.zdim() << std::endl;
 
  Values values { devil_value, grid };
  Gradients gradients { devil_gradient, grid };
 
  // Below is equivalent to:
  //   Domain domain { grid, values, gradients };
  Domain domain = CGAL::Isosurfacing::create_dual_contouring_domain_3(grid, values, gradients);
 
  Point_range points;
  Polygon_range triangles;
 
  // run dual contouring isosurfacing
  std::cout << "Running Dual Contouring with isovalue = " << isovalue << std::endl;
  CGAL::Isosurfacing::dual_contouring<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles,
                                                                       CGAL::parameters::do_not_triangulate_faces(true)
                                                                                        .constrain_to_cell(false));
 
  std::cout << "Output #vertices: " << points.size() << std::endl;
  std::cout << "Output #triangles: " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("dual_contouring.off", points, triangles);
 
  std::cout << "Done" << std::endl;
 
  return EXIT_SUCCESS;
}

Figure 61.7 Results of the Dual Contouring algorithm: untriangulated (left column) or triangulated (right column), unconstrained vertex location (top row) or constrained vertex location (bottom row).

Dual Contouring using Octree

The following example shows the use of an octree for dual contouring or marching cubes.

File Isosurfacing_3/dual_contouring_octree.cpp

#include <CGAL/Simple_cartesian.h>
 
#include <CGAL/Isosurfacing_3/dual_contouring_3.h>
#include <CGAL/Isosurfacing_3/Dual_contouring_domain_3.h>
#include <CGAL/Isosurfacing_3/marching_cubes_3.h>
#include <CGAL/Isosurfacing_3/Marching_cubes_domain_3.h>
#include <CGAL/Isosurfacing_3/Value_function_3.h>
#include <CGAL/Isosurfacing_3/Gradient_function_3.h>
#include <CGAL/Isosurfacing_3/Octree_partition.h>
 
#include <CGAL/IO/polygon_soup_io.h>
#include <CGAL/Real_timer.h>
 
#include <cmath>
#include <iostream>
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Vector = typename Kernel::Vector_3;
using Point = typename Kernel::Point_3;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
using Octree = CGAL::Octree<Kernel, std::vector<typename Kernel::Point_3> >;
using Values = CGAL::Isosurfacing::Value_function_3<Octree>;
using Gradients = CGAL::Isosurfacing::Gradient_function_3<Octree>;
using MC_Domain = CGAL::Isosurfacing::Marching_cubes_domain_3<Octree, Values>;
using Domain = CGAL::Isosurfacing::Dual_contouring_domain_3<Octree, Values, Gradients>;
 
// Refine one of the octant
struct Refine_one_eighth
{
  std::size_t min_depth_;
  std::size_t max_depth_;
 
  std::size_t octree_dim_;
 
  Refine_one_eighth(std::size_t min_depth,
                    std::size_t max_depth)
    : min_depth_(min_depth),
      max_depth_(max_depth)
  {
    octree_dim_ = std::size_t(1) << max_depth_;
  }
 
  Octree::Global_coordinates uniform_coordinates(const Octree::Node_index& node_index, const Octree& octree) const
  {
    auto coords = octree.global_coordinates(node_index);
    const std::size_t depth_factor = std::size_t(1) << (max_depth_ - octree.depth(node_index));
    for(int i=0; i < 3; ++i)
      coords[i] *= uint32_t(depth_factor);
 
    return coords;
  }
 
  bool operator()(const Octree::Node_index& ni, const Octree& octree) const
  {
    if(octree.depth(ni) < min_depth_)
      return true;
 
    if(octree.depth(ni) == max_depth_)
      return false;
 
    auto leaf_coords = uniform_coordinates(ni, octree);
 
    if(leaf_coords[0] >= octree_dim_ / 2)
      return false;
 
    if(leaf_coords[1] >= octree_dim_ / 2)
      return false;
 
    if(leaf_coords[2] >= octree_dim_ / 2)
      return false;
 
    return true;
  }
};
 
auto sphere_function = [](const Point& p) -> FT
{
  return std::sqrt(p.x()*p.x() + p.y()*p.y() + p.z()*p.z());
};
 
auto sphere_gradient = [](const Point& p) -> Vector
{
  const Vector g = p - CGAL::ORIGIN;
  return g / std::sqrt(g.squared_length());
};
 
int main(int argc, char** argv)
{
  const FT isovalue = (argc > 1) ? std::stod(argv[1]) : 0.8;
 
  const CGAL::Bbox_3 bbox{-1., -1., -1.,  1., 1., 1.};
  std::vector<Kernel::Point_3> bbox_points { {bbox.xmin(), bbox.ymin(), bbox.zmin()},
    { bbox.xmax(), bbox.ymax(), bbox.zmax() } };
 
  CGAL::Real_timer timer;
  timer.start();
 
  Octree octree(bbox_points);
  Refine_one_eighth split_predicate(3, 5);
  octree.refine(split_predicate);
 
  // fill up values and gradients
  Values values { sphere_function, octree };
  Gradients gradients { sphere_gradient, octree };
  Domain domain { octree, values, gradients };
 
  // output containers
  Point_range points;
  Polygon_range triangles;
 
  // run Dual Contouring
  CGAL::Isosurfacing::dual_contouring<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles, CGAL::parameters::do_not_triangulate_faces(true));
 
  // run Marching Cubes
  // ToDo: Does not yet work with topologically correct marching cubes
  // MC_Domain mcdomain{ octree, values };
  // CGAL::Isosurfacing::marching_cubes<CGAL::Parallel_if_available_tag>(mcdomain, isovalue, points, triangles);
 
  timer.stop();
 
  std::ofstream oo("octree2.polylines.txt");
  oo.precision(17);
  octree.dump_to_polylines(oo);
 
  std::cout << "Running Dual Contouring with isovalue = " << isovalue << std::endl;
 
  std::cout << "Output #vertices (DC): " << points.size() << std::endl;
  std::cout << "Output #triangles (DC): " << triangles.size() << std::endl;
  std::cout << "Elapsed time: " << timer.time() << " seconds" << std::endl;
  CGAL::IO::write_polygon_soup("dual_contouring_octree.off", points, triangles);
 
  std::cout << "Done" << std::endl;
 
  return EXIT_SUCCESS;
}

Implicit Data

The following example shows the usage of Marching Cubes and Dual Contouring algorithms to extract an isosurface. The domain is implicit and describes the unit sphere by the distance to its center (set to the origin) as an implicit 3D value field.

File Isosurfacing_3/contouring_implicit_data.cpp

#include <CGAL/Simple_cartesian.h>
 
#include <CGAL/Isosurfacing_3/Cartesian_grid_3.h>
#include <CGAL/Isosurfacing_3/dual_contouring_3.h>
#include <CGAL/Isosurfacing_3/Dual_contouring_domain_3.h>
#include <CGAL/Isosurfacing_3/Value_function_3.h>
#include <CGAL/Isosurfacing_3/Gradient_function_3.h>
#include <CGAL/Isosurfacing_3/marching_cubes_3.h>
#include <CGAL/Isosurfacing_3/Marching_cubes_domain_3.h>
 
#include <CGAL/Bbox_3.h>
#include <CGAL/Real_timer.h>
#include <CGAL/IO/polygon_soup_io.h>
 
#include <array>
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Point = typename Kernel::Point_3;
using Vector = typename Kernel::Vector_3;
 
// using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel, CGAL::Isosurfacing::Do_not_cache_vertex_locations>;
using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel, CGAL::Isosurfacing::Cache_vertex_locations>;
using Values = CGAL::Isosurfacing::Value_function_3<Grid>;
using Gradients = CGAL::Isosurfacing::Gradient_function_3<Grid>;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
// ---
const FT alpha = 5.01;
 
auto iwp_value = [](const Point& point)
{
  const FT x = alpha * (point.x() + FT(1.0)) * CGAL_PI;
  const FT y = alpha * (point.y() + FT(1.0)) * CGAL_PI;
  const FT z = alpha * (point.z() + FT(1.0)) * CGAL_PI;
  return cos(x)*cos(y) + cos(y)*cos(z) + cos(z)*cos(x) - cos(x)*cos(y)*cos(z);  // isovalue = 0
};
 
auto iwp_gradient = [](const Point& point)
{
  const FT x = alpha * (point.x() + FT(1.0)) * CGAL_PI;
  const FT y = alpha * (point.y() + FT(1.0)) * CGAL_PI;
  const FT z = alpha * (point.z() + FT(1.0)) * CGAL_PI;
 
  const FT gx = CGAL_PI * alpha * sin(x) * (cos(y) * (cos(z) - FT(1.0)) - cos(z));
  const FT gy = CGAL_PI * alpha * sin(y) * (cos(x) * (cos(z) - FT(1.0)) - cos(z));
  const FT gz = CGAL_PI * alpha * sin(z) * (cos(x) * (cos(y) - FT(1.0)) - cos(y));
  return Vector(gx, gy, gz);
};
 
void run_marching_cubes(const Grid& grid,
                        const FT isovalue)
{
  using Domain = CGAL::Isosurfacing::Marching_cubes_domain_3<Grid, Values>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Marching Cubes with isovalue = " << isovalue << std::endl;
 
  CGAL::Real_timer timer;
  timer.start();
 
  // fill up values
  Values values { iwp_value, grid };
  Domain domain { grid, values };
 
  // output containers
  Point_range points;
  Polygon_range triangles;
 
  // run Marching Cubes
  CGAL::Isosurfacing::marching_cubes<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles);
 
  timer.stop();
 
  std::cout << "Output #vertices (MC): " << points.size() << std::endl;
  std::cout << "Output #triangles (MC): " << triangles.size() << std::endl;
  std::cout << "Elapsed time: " << timer.time() << " seconds" << std::endl;
  CGAL::IO::write_polygon_soup("marching_cubes_implicit.off", points, triangles);
}
 
void run_dual_contouring(const Grid& grid,
                         const FT isovalue)
{
  using Domain = CGAL::Isosurfacing::Dual_contouring_domain_3<Grid, Values, Gradients>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Dual Contouring with isovalue = " << isovalue << std::endl;
 
  CGAL::Real_timer timer;
  timer.start();
 
  // fill up values and gradients
  Values values { iwp_value, grid };
  Gradients gradients { iwp_gradient, grid };
  Domain domain { grid, values, gradients };
 
  // output containers
  Point_range points;
  Polygon_range triangles;
 
  // run Dual Contouring
  CGAL::Isosurfacing::dual_contouring<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles,
                                                                       CGAL::parameters::do_not_triangulate_faces(true));
 
  timer.stop();
 
  std::cout << "Output #vertices (DC): " << points.size() << std::endl;
  std::cout << "Output #triangles (DC): " << triangles.size() << std::endl;
  std::cout << "Elapsed time: " << timer.time() << " seconds" << std::endl;
  CGAL::IO::write_polygon_soup("dual_contouring_implicit.off", points, triangles);
}
 
int main(int argc, char** argv)
{
  const FT isovalue = (argc > 1) ? std::stod(argv[1]) : 0.;
 
  const CGAL::Bbox_3 bbox{-1, -1, -1,  1, 1, 1};
  const FT step = 0.02;
  const Vector spacing { step, step, step };
  Grid grid { bbox, spacing };
 
  std::cout << "Span: " << grid.span() << std::endl;
  std::cout << "Cell dimensions: " << grid.spacing()[0] << " " << grid.spacing()[1] << " " << grid.spacing()[2] << std::endl;
  std::cout << "Cell #: " << grid.xdim() << ", " << grid.ydim() << ", " << grid.zdim() << std::endl;
 
  run_marching_cubes(grid, isovalue);
 
  run_dual_contouring(grid, isovalue);
 
  std::cout << "Done" << std::endl;
 
  return EXIT_SUCCESS;
}

Discrete Data

In the following example, the input data is sampled at the vertices of a grid, and interpolated.

File Isosurfacing_3/contouring_discrete_data.cpp

#include <CGAL/Simple_cartesian.h>
 
#include <CGAL/Isosurfacing_3/Cartesian_grid_3.h>
#include <CGAL/Isosurfacing_3/dual_contouring_3.h>
#include <CGAL/Isosurfacing_3/Dual_contouring_domain_3.h>
#include <CGAL/Isosurfacing_3/Interpolated_discrete_gradients_3.h>
#include <CGAL/Isosurfacing_3/Interpolated_discrete_values_3.h>
#include <CGAL/Isosurfacing_3/marching_cubes_3.h>
#include <CGAL/Isosurfacing_3/Marching_cubes_domain_3.h>
 
#include <CGAL/IO/polygon_soup_io.h>
 
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Point = typename Kernel::Point_3;
using Vector = typename Kernel::Vector_3;
 
using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel>;
using Values = CGAL::Isosurfacing::Interpolated_discrete_values_3<Grid>;
using Gradients = CGAL::Isosurfacing::Interpolated_discrete_gradients_3<Grid>;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
namespace IS = CGAL::Isosurfacing;
 
void run_marching_cubes(const Grid& grid,
                        const FT isovalue)
{
  using Domain = IS::Marching_cubes_domain_3<Grid, Values, IS::Linear_interpolation_edge_intersection>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Marching Cubes with isovalue = " << isovalue << std::endl;
 
  // fill up values
  Values values { grid };
 
  for(std::size_t i=0; i<grid.xdim(); ++i) {
    for(std::size_t j=0; j<grid.ydim(); ++j) {
      for(std::size_t k=0; k<grid.zdim(); ++k)
      {
        const Point& p = grid.point(i,j,k);
        const FT d = sqrt(CGAL::squared_distance(p, Point(CGAL::ORIGIN)));
        values(i,j,k) = d;
      }
    }
  }
 
  Domain domain { grid, values };
 
  Point_range points;
  Polygon_range triangles;
 
  // run marching cubes isosurfacing
  IS::marching_cubes<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles);
 
  std::cout << "Output #vertices: " << points.size() << std::endl;
  std::cout << "Output #triangles: " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("marching_cubes_discrete.off", points, triangles);
}
 
void run_dual_contouring(const Grid& grid,
                         const FT isovalue)
{
  using Domain = IS::Dual_contouring_domain_3<Grid, Values, Gradients, IS::Linear_interpolation_edge_intersection>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Dual Contouring with isovalue = " << isovalue << std::endl;
 
  // fill up values and gradients
  Values values { grid };
  Gradients gradients { grid };
 
  for(std::size_t i=0; i<grid.xdim(); ++i) {
    for(std::size_t j=0; j<grid.ydim(); ++j) {
      for(std::size_t k=0; k<grid.zdim(); ++k)
      {
        const Point& p = grid.point(i,j,k);
        const FT d = sqrt(CGAL::squared_distance(p, Point(CGAL::ORIGIN)));
        values(i,j,k) = d;
 
        if(d != 0)
          gradients(i,j,k) = Vector(CGAL::ORIGIN, p) / d;
        else
          gradients(i,j,k) = CGAL::NULL_VECTOR;
      }
    }
  }
 
  // If the gradient was not known analytically, we could use:
  // - Finite_difference_gradient_3 to use finite difference to compute it from values;
  // - the function below to use finite difference _and_ store the values at the grid vertices
  //     gradients.compute_discrete_gradients(values);
 
  Domain domain { grid, values, gradients };
 
  Point_range points;
  Polygon_range triangles;
 
  // run dual contouring isosurfacing
  IS::dual_contouring<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles);
 
  std::cout << "Output #vertices: " << points.size() << std::endl;
  std::cout << "Output #triangles: " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("dual_contouring_discrete.off", points, triangles);
}
 
int main(int argc, char** argv)
{
  const FT isovalue = (argc > 1) ? std::stod(argv[1]) : 0.8;
 
  // create bounding box and grid
  const CGAL::Bbox_3 bbox { -1., -1., -1., 1., 1., 1. };
  Grid grid { bbox, CGAL::make_array<std::size_t>(30, 30, 30) };
 
  std::cout << "Span: " << grid.span() << std::endl;
  std::cout << "Cell dimensions: " << grid.spacing()[0] << " " << grid.spacing()[1] << " " << grid.spacing()[2] << std::endl;
  std::cout << "Cell #: " << grid.xdim() << ", " << grid.ydim() << ", " << grid.zdim() << std::endl;
 
  run_marching_cubes(grid, isovalue);
 
  run_dual_contouring(grid, isovalue);
 
  std::cout << "Done" << std::endl;
 
  return EXIT_SUCCESS;
}

3D Image

The following example shows how to load data from an Image_3, and generates an isosurface from this voxel data.

File Isosurfacing_3/contouring_inrimage.cpp

#include <CGAL/Simple_cartesian.h>
 
#include <CGAL/Isosurfacing_3/Cartesian_grid_3.h>
#include <CGAL/Isosurfacing_3/dual_contouring_3.h>
#include <CGAL/Isosurfacing_3/Dual_contouring_domain_3.h>
#include <CGAL/Isosurfacing_3/Finite_difference_gradient_3.h>
#include <CGAL/Isosurfacing_3/Interpolated_discrete_values_3.h>
#include <CGAL/Isosurfacing_3/marching_cubes_3.h>
#include <CGAL/Isosurfacing_3/Marching_cubes_domain_3.h>
 
#include <CGAL/Image_3.h>
 
#include <CGAL/Isosurfacing_3/IO/Image_3.h>
#include <CGAL/IO/polygon_soup_io.h>
 
#include <iostream>
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Point = typename Kernel::Point_3;
 
using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel>;
using Values = CGAL::Isosurfacing::Interpolated_discrete_values_3<Grid>;
using Gradients = CGAL::Isosurfacing::Finite_difference_gradient_3<Kernel>;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
namespace IS = CGAL::Isosurfacing;
 
void run_marching_cubes(const Grid& grid,
                        const FT isovalue,
                        const Values& values)
{
  using Domain = IS::Marching_cubes_domain_3<Grid, Values, IS::Linear_interpolation_edge_intersection>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Marching Cubes with isovalue = " << isovalue << std::endl;
 
  // fill up values
 
  // create a domain from the grid
  Domain domain { grid, values };
 
  // prepare collections for the output indexed soup
  Point_range points;
  Polygon_range triangles;
 
  // execute marching cubes
  IS::marching_cubes<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles);
 
  std::cout << "Output #vertices: " << points.size() << std::endl;
  std::cout << "Output #triangles: " << triangles.size() << std::endl;
 
  // save output indexed mesh to a file, in the OFF format
  CGAL::IO::write_polygon_soup("marching_cubes_inrimage.off", points, triangles);
}
 
void run_dual_contouring(const Grid& grid,
                         const FT isovalue,
                         const Values& values)
{
  using Domain = IS::Dual_contouring_domain_3<Grid, Values, Gradients, IS::Linear_interpolation_edge_intersection>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Dual Contouring with isovalue = " << isovalue << std::endl;
 
  // fill up values and gradients
  const FT step = CGAL::approximate_sqrt(grid.spacing().squared_length()) * 0.01; // finite difference step
  Gradients gradients { values, step };
  Domain domain { grid, values, gradients };
 
  Point_range points;
  Polygon_range triangles;
 
  // run dual contouring isosurfacing
  IS::dual_contouring<CGAL::Parallel_if_available_tag>(domain, isovalue, points, triangles);
 
  std::cout << "Output #vertices: " << points.size() << std::endl;
  std::cout << "Output #triangles: " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("dual_contouring_inrimage.off", points, triangles);
}
 
int main(int argc, char* argv[])
{
  const std::string fname = (argc > 1) ? argv[1] : CGAL::data_file_path("images/skull_2.9.inr");
  const FT isovalue = (argc > 2) ? std::stod(argv[2]) : - 2.9;
 
  // load volumetric image from a file
  CGAL::Image_3 image;
  if(!image.read(fname))
  {
    std::cerr << "Error: Cannot read image file " << fname << std::endl;
    return EXIT_FAILURE;
  }
 
  // convert image to a Cartesian grid
  Grid grid;
  Values values { grid }; // 'values' keeps a reference to the grid
  if(!IS::IO::convert_image_to_grid(image, grid, values))
  {
    std::cerr << "Error: Cannot convert image to Cartesian grid" << std::endl;
    return EXIT_FAILURE;
  }
 
  std::cout << "Span: " << grid.span() << std::endl;
  std::cout << "Cell dimensions: " << grid.spacing()[0] << " " << grid.spacing()[1] << " " << grid.spacing()[2] << std::endl;
  std::cout << "Cell #: " << grid.xdim() << ", " << grid.ydim() << ", " << grid.zdim() << std::endl;
 
  run_marching_cubes(grid, isovalue, values);
 
  run_dual_contouring(grid, isovalue, values);
 
  return EXIT_SUCCESS;
}

Figure 61.8 Results of the Topologically Correct Marching Cubes algorithm for different isovalues (1, 2, and 2.9) on the skull model.

Offset Mesh

The following example illustrates how to generate a mesh approximating a signed offset to an input closed surface mesh. The input mesh is stored into an AABB_tree data structure to provide fast distance queries. Via the Side_of_triangle_mesh functor, the sign of the distance field is made negative inside the mesh.

File Isosurfacing_3/contouring_mesh_offset.cpp

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Surface_mesh.h>
 
#include <CGAL/Isosurfacing_3/Cartesian_grid_3.h>
#include <CGAL/Isosurfacing_3/dual_contouring_3.h>
#include <CGAL/Isosurfacing_3/Dual_contouring_domain_3.h>
#include <CGAL/Isosurfacing_3/Value_function_3.h>
#include <CGAL/Isosurfacing_3/Finite_difference_gradient_3.h>
#include <CGAL/Isosurfacing_3/marching_cubes_3.h>
#include <CGAL/Isosurfacing_3/Marching_cubes_domain_3.h>
 
#include <CGAL/AABB_face_graph_triangle_primitive.h>
#include <CGAL/AABB_traits_3.h>
#include <CGAL/AABB_tree.h>
#include <CGAL/Bbox_3.h>
#include <CGAL/Polygon_mesh_processing/bbox.h>
#include <CGAL/Side_of_triangle_mesh.h>
 
#include <CGAL/boost/graph/IO/polygon_mesh_io.h>
#include <CGAL/IO/polygon_soup_io.h>
 
#include <iostream>
#include <string>
#include <vector>
 
using Kernel = CGAL::Simple_cartesian<double>;
using FT = typename Kernel::FT;
using Point = typename Kernel::Point_3;
using Vector = typename Kernel::Vector_3;
 
using Mesh = CGAL::Surface_mesh<Point>;
 
using Grid = CGAL::Isosurfacing::Cartesian_grid_3<Kernel>;
using Values = CGAL::Isosurfacing::Value_function_3<Grid>;
using Gradients = CGAL::Isosurfacing::Finite_difference_gradient_3<Kernel>;
 
using Point_range = std::vector<Point>;
using Polygon_range = std::vector<std::vector<std::size_t> >;
 
struct Offset_oracle
{
  using Primitive = CGAL::AABB_face_graph_triangle_primitive<Mesh>;
  using Traits = CGAL::AABB_traits_3<Kernel, Primitive>;
  using Tree = CGAL::AABB_tree<Traits>;
 
private:
  const bool is_closed;
  const Tree tree;
  CGAL::Side_of_triangle_mesh<Mesh, Kernel> sotm;
 
public:
  Offset_oracle(const Mesh& mesh)
    : is_closed(CGAL::is_closed(mesh)), tree(mesh.faces_begin(), mesh.faces_end(), mesh), sotm(mesh)
  { }
 
  FT distance(const Point& p) const
  {
    const Point cp = tree.closest_point(p);
    FT d = sqrt((p - cp).squared_length());
 
    if(is_closed && sotm(p) == (CGAL::ON_BOUNDED_SIDE))
      d *= -1.0;
 
    return d;
  }
};
 
void run_marching_cubes(const Grid& grid,
                         const FT offset_value,
                         const Offset_oracle& offset_oracle)
{
  using Domain = CGAL::Isosurfacing::Marching_cubes_domain_3<Grid, Values>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Marching Cubes with offset value = " << offset_value << std::endl;
 
  // fill up values
  auto mesh_distance = [&offset_oracle](const Point& p) { return offset_oracle.distance(p); };
  Values values { mesh_distance, grid };
  Domain domain { grid, values };
 
  Point_range points;
  Polygon_range triangles;
 
  // run marching cubes
  std::cout << "Running Marching Cubes with isovalue = " << offset_value << std::endl;
  CGAL::Isosurfacing::marching_cubes<CGAL::Parallel_if_available_tag>(domain, offset_value, points, triangles);
 
  std::cout << "Output #vertices (MC): " << points.size() << std::endl;
  std::cout << "Output #triangles (MC): " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("marching_cubes_offsets.off", points, triangles);
}
 
void run_dual_contouring(const Grid& grid,
                         const FT offset_value,
                         const Offset_oracle& offset_oracle)
{
  using Domain = CGAL::Isosurfacing::Dual_contouring_domain_3<Grid, Values, Gradients>;
 
  std::cout << "\n ---- " << std::endl;
  std::cout << "Running Dual Contouring with offset value = " << offset_value << std::endl;
 
  // fill up values and gradients
  auto mesh_distance = [&offset_oracle](const Point& p) { return offset_oracle.distance(p); };
 
  const FT step = CGAL::approximate_sqrt(grid.spacing().squared_length()) * 0.01;
 
  Values values { mesh_distance, grid };
  Gradients gradients { values, step };
  Domain domain { grid, values, gradients };
 
  // output containers
  Point_range points;
  Polygon_range triangles;
 
  // run dual contouring
  std::cout << "Running Dual Contouring with isovalue = " << offset_value << std::endl;
  CGAL::Isosurfacing::dual_contouring<CGAL::Parallel_if_available_tag>(
                        domain, offset_value, points, triangles,
                        CGAL::parameters::do_not_triangulate_faces(true));
 
  std::cout << "Output #vertices (DC): " << points.size() << std::endl;
  std::cout << "Output #triangles (DC): " << triangles.size() << std::endl;
  CGAL::IO::write_polygon_soup("dual_contouring_mesh_offset.off", points, triangles);
}
 
int main(int argc, char** argv)
{
  const std::string filename = (argc > 1) ? argv[1] : CGAL::data_file_path("meshes/cross.off");
  const FT offset_value = (argc > 2) ? std::stod(argv[2]) : 0.2;
 
  if(offset_value < 0)
  {
    std::cerr << "Offset value must be positive" << std::endl;
    return EXIT_FAILURE;
  }
 
  Mesh mesh;
  if(!CGAL::IO::read_polygon_mesh(filename, mesh) || is_empty(mesh))
  {
    std::cerr << "Could not read input mesh" << std::endl;
    return EXIT_FAILURE;
  }
 
  if(CGAL::is_closed(mesh))
    std::cout << "Input mesh is closed - using signed distance offset" << std::endl;
  else
    std::cout << "Input mesh is not closed - using unsigned distance offset" << std::endl;
 
  // construct loose bounding box from input mesh
  CGAL::Bbox_3 bbox = CGAL::Polygon_mesh_processing::bbox(mesh);
 
  const FT diag_length = sqrt(CGAL::square(bbox.xmax() - bbox.xmin()) +
                              CGAL::square(bbox.ymax() - bbox.ymin()) +
                              CGAL::square(bbox.zmax() - bbox.zmin()));
  const FT loose_offset = offset_value + 0.1 * diag_length;
 
  Vector aabb_increase_vec = Vector(loose_offset, loose_offset, loose_offset);
  bbox += (Point(bbox.xmax(), bbox.ymax(), bbox.zmax()) + aabb_increase_vec).bbox();
  bbox += (Point(bbox.xmin(), bbox.ymin(), bbox.zmin()) - aabb_increase_vec).bbox();
 
  const int nv = 15;
 
  Grid grid { bbox, CGAL::make_array<std::size_t>(nv, nv, nv) };
 
  std::cout << "Span: " << grid.span() << std::endl;
  std::cout << "Cell dimensions: " << grid.spacing()[0] << " " << grid.spacing()[1] << " " << grid.spacing()[2] << std::endl;
  std::cout << "Cell #: " << grid.xdim() << ", " << grid.ydim() << ", " << grid.zdim() << std::endl;
 
  Offset_oracle offset_oracle(mesh);
 
  run_marching_cubes(grid, offset_value, offset_oracle);
 
  run_dual_contouring(grid, offset_value, offset_oracle);
 
  return EXIT_SUCCESS;
}

Design and Implementation History

The development of this package started during the 2022 Google Summer of Code, with the contribution of Julian Stahl, mentored by Daniel Zint and Pierre Alliez, providing a first implementation of Marching Cubes, Topologically Correct Marching Cubes, and Dual Contouring. Marching Cubes tables were provided by Roberto Grosso (FAU Erlangen-Nürnberg). Mael Rouxel-Labbé worked on improving the initial Dual Contouring implementation, and on the first complete version of the package.