User Manual

• 1 Introduction
• 2 API
• 3 Performance
• 4 Implementation
• 5 Examples
• 5.1 Decision for 2D Polylines
• 5.2 Distance Computation for 3D Polylines
• 5.3 Distance Computation for dD Polylines
• 5.4 Searching Close Curves
• 5.5 Image Credits
• 5.6 Implementation History

Authors

André Nusser, Marvin Künnemann, and Karl Bringmann

This package provides the means to (approximately) compute the Fréchet distance between two polylines as well as a near neighbor data structure for polylines under the Fréchet distance, both in d-dimensional Euclidean space. A polyline is defined by a sequence of points where we interpolate linearly in-between each pair of consecutive points. In order to determine the Fréchet distance, an exact decision algorithm as well as a function that approximates the Fréchet distance arbitrarily well is included in the package. The approximation algorithm is simply a binary search that repeatedly calls the decision algorithm, hence, if possible, the latter should preferably be used when optimizing for performance.

1 Introduction

The Fréchet distance is a classical dissimilarity measure between polylines. Its advantages over other measures are that it both considers the polylines as continuous objects and takes into account the ordering of the points. Intuitively, the Fréchet distance is commonly explained as follows: Imagine a human walking on one polyline while a dog walks on the other polyline, they are connected by a leash, and they are only allowed to walk forward. The Fréchet distance is the shortest leash length that allows the human and the dog to jointly walk from start to end on their respective trajectories where they can each vary their speed arbitrarily. The Fréchet distance is a metric. This implies that it is symmetric and that two polylines have distance zero if and only if they are equal (after removing redundant vertices).

The applications of this distance measure are plenty, for example:

• comparing the GPS traces of migrating animals to find the different routes that are being used
• measuring the similarity between movement patterns recorded via motion capture
• perform map matching to match a GPS trace to a transportation network

2 API

The main entry points are the following functions and classes:

• The function bounded_error_Frechet_distance() computes an approximation of the Fréchet distance between two polylines, up to a given approximation error. It returns an interval that contains the true distance.
• The function is_Frechet_distance_larger() decides if the Fréchet distance between two polylines is larger than a given bound.
• The class Frechet_distance::Neighbor_search stores a set of polylines and offers a query functions to find polylines closer to a query curve than a given bound.

Both functions and the class have as template parameter a traits class defining the dimension and the point type. The traits classes have as template parameter a kernel, model of the concept Kernel. In case the static constant Has_filtered_predicates of the kernel is true, the functions combine interval arithmetic with a fallback to exact computing in case comparisons of intervals are uncertain. This means for Simple_cartesian<double> that there are no guarantees, for Simple_cartesian<Exact_rational> that all computations are performed with exact rationals, and for kernels such as Exact_predicates_inexact_constructions_kernel, Exact_predicates_exact_constructions_kernel, as well as Epick_d and Epeck_d, the computation is filtered and hence both fast and guaranteed to be correct.

3 Performance

The performance of the algorithm is quadratic in the number of vertices in the worst case. For all kernels with filtered predicates the performance is roughly the same, the overhead of using interval arithmetic is negligible. The algorithm is not concerned by the curse of dimensionality. The running time increases when the curves are closer or when the bound for the approximation error becomes smaller. For a very detailed analysis in practice we refer to the journal paper entitled Walking the Dog Fast in Practice: Algorithm Engineering of the Fréchet Distance [3].

4 Implementation

The algorithms in this package are an adaption of the implementation devised by Bringmann et al. ([2] and [3]). In particular, the implementation can decide non-difficult cases very fast while for difficult cases it still has the quadratic running time guarantee of the classical Fréchet distance algorithm by Alt and Godau [1]. This is achieved by using fast bounding box filtering methods and a divide and conquer algorithm with pruning rules on the free-space diagram.

5 Examples

In the examples we use different kernels to illustrate that the functions can be used with either inexact or exact kernels.

5.1 Decision for 2D Polylines

The following example shows how we can use is_Frechet_distance_larger() to determines if the Frechet distance between two polylines is larger than a given distance bound.

File Frechet_distance/Frechet_distance_2.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Frechet_distance.h>
#include <CGAL/IO/WKT.h>
 
#include <ostream>
#include <fstream>
 
using Kernel = CGAL::Exact_predicates_inexact_constructions_kernel;
using Point = Kernel::Point_2;
 
int main(int argc, char* argv[])
{
    std::vector<Point> polylineA, polylineB;
    {
      std::ifstream in((argc > 1) ? argv[1] : CGAL::data_file_path("wkt/LetterA.wkt"));
      CGAL::IO::read_linestring_WKT(in, polylineA);
    }
    {
      std::ifstream in((argc > 1) ? argv[2] : CGAL::data_file_path("wkt/LetterAbis.wkt"));
      CGAL::IO::read_linestring_WKT(in, polylineB);
    }
    bool res = CGAL::is_Frechet_distance_larger(polylineA, polylineB, 0.001);
    std::cout << std::boolalpha << res << std::endl;
    return 0;
}

5.2 Distance Computation for 3D Polylines

The following example shows how we can compute the Fréchet distance up to a given error bound on two polylines in 3-dimensional Euclidean space using bounded_error_Frechet_distance(). As we use Simple_cartesian<double> the algorithm uses plain floating point arithmetic without guarantees for correctness.

File Frechet_distance/Frechet_distance_3.cpp

#include <CGAL/Frechet_distance.h>
#include <CGAL/Simple_cartesian.h>
#include <CGAL/IO/WKT.h>
 
#include <ostream>
#include <fstream>
 
using Kernel = CGAL::Simple_cartesian<double>;
using Point = Kernel::Point_3;
 
int main(int argc, char* argv[])
{
    std::vector<Point> polylineA, polylineB;
    {
      std::ifstream in((argc > 1) ? argv[1] : CGAL::data_file_path("wkt/moebius.wkt"));
      CGAL::IO::read_linestring_WKT(in, polylineA);
    }
    {
      std::ifstream in((argc > 2) ? argv[2] : CGAL::data_file_path("wkt/moebius2.wkt"));
      CGAL::IO::read_linestring_WKT(in, polylineB);
    }
 
    std::pair<double, double> res = CGAL::bounded_error_Frechet_distance(polylineA, polylineB, 0.000001);
    std::cout << "The Frechet distance between the polylines is between " <<  res.first << " and " << res.second << std::endl;
    return 0;
}

5.3 Distance Computation for dD Polylines

The following example shows how we can compute the Fréchet distance up to a given error bound on two polylines in 4-dimensional Euclidean space using bounded_error_Frechet_distance().

File Frechet_distance/Frechet_distance_d.cpp

#include <CGAL/Epick_d.h>
#include <CGAL/Frechet_distance.h>
 
#include <iostream>
#include <vector>
 
using Kernel = CGAL::Epick_d<CGAL::Dimension_tag<4>>;
using Point = Kernel::Point_d;
 
int main()
{
    std::array<Point,4> polylineA = { Point(0,0,0,0), Point(1,0,0,0), Point(1,1,0,1),Point(1,1,1,0)};
    std::array<Point,4> polylineB = { Point(0,0,0,0), Point(1,0,0,0), Point(1,1,0,0),Point(1,1,1,0)};
 
    std::pair<double, double> res = CGAL::bounded_error_Frechet_distance(polylineA, polylineB, 0.000001);
    std::cout << "The Frechet distance between the polylines is between " <<  res.first << " and " << res.second << std::endl;
    return 0;
}

5.4 Searching Close Curves

The following example shows how to store many curves in a data structure and to find all curves closer than a distance bound to a query curve.

File Frechet_distance/Frechet_DS_3.cpp

#include <CGAL/Frechet_distance.h>
#include <CGAL/Frechet_distance_traits_3.h>
#include <CGAL/Frechet_distance/Neighbor_search.h>
#include <CGAL/Simple_cartesian.h>
#include <CGAL/IO/WKT.h>
 
#include <ostream>
#include <fstream>
#include <filesystem>
 
using Kernel = CGAL::Simple_cartesian<double>;
using Traits = CGAL::Frechet_distance_traits_3<Kernel>;
using Point = Traits::Point_d;
using Curve = std::vector<Point>;
using Curves = std::vector<Curve>;
 
int main()
{
 
  Curves curves;
  const std::filesystem::path data{"./data_3d"};
  for (auto const& dir_entry : std::filesystem::directory_iterator{data}){
    std::ifstream in(dir_entry.path());
    curves.push_back(Curve());
    CGAL::IO::read_linestring_WKT(in, curves.back());
  }
 
  Curve query = curves.back();
  curves.pop_back();
 
  CGAL::Frechet_distance::Neighbor_search<Curve, Traits> ds(curves);
 
  for(const Curve& c : curves){
    std::pair<double, double> res = CGAL::bounded_error_Frechet_distance(c, query, 0.000001);
    std::cout << "The Frechet distance between the polylines is between " <<  res.first << " and " << res.second << std::endl;
  }
  double distance = 16;
  std::vector<std::size_t> result = ds.get_close_curves(query, distance);
 
  std::cout << result.size() << " curves at Frechet distance closer than " << distance << std::endl;
  return 0;
}

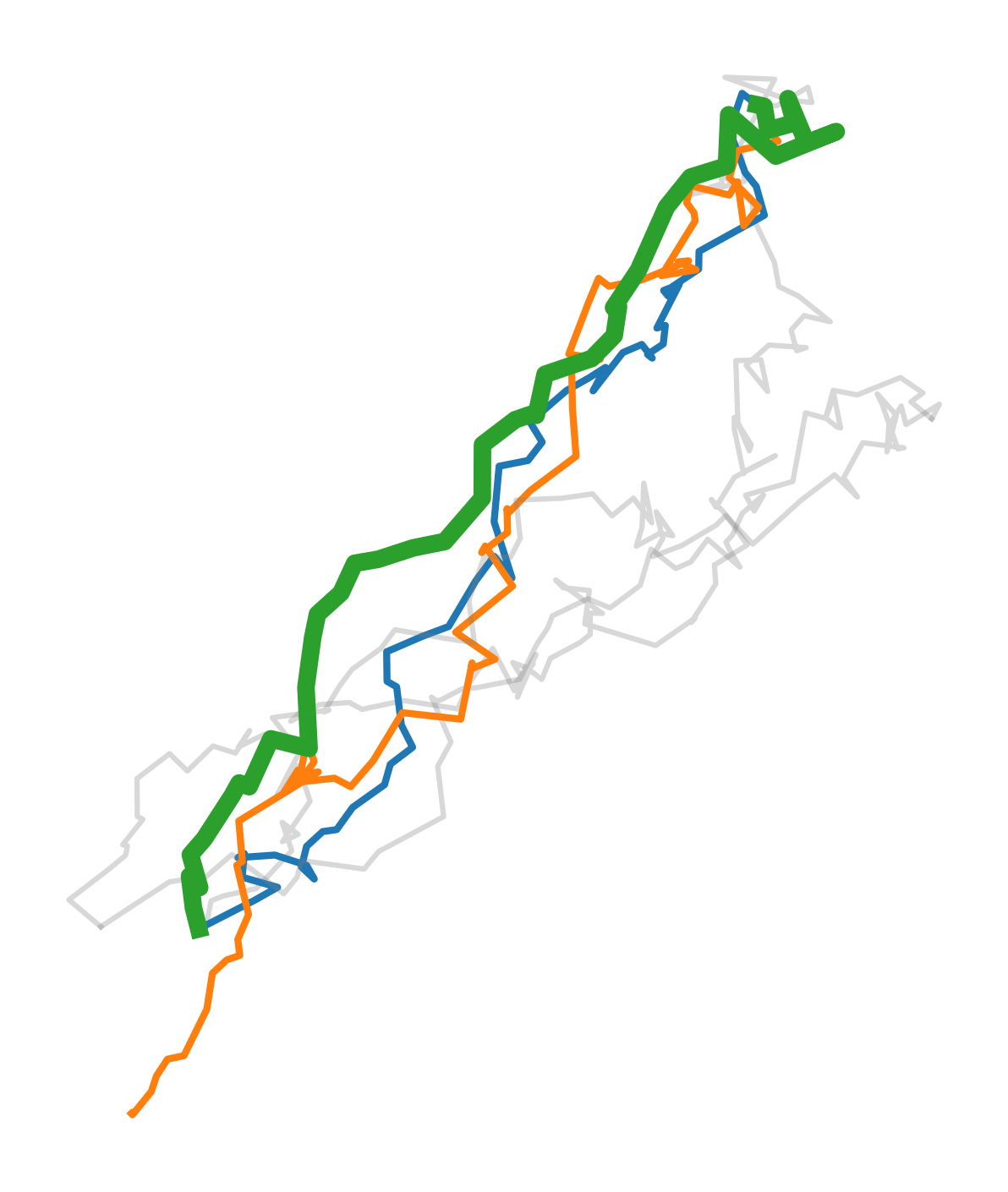
In the example below, we can see a query where:

• the query polyline is in bold green
• the query distance is 16
• the colorfull polylines are in distance at most 16 from the query and are therefore returned
• the light gray polylines are filtered out early on and no significant computation is performed on them
• the dark gray polyline is not filtered out early on but only later by our exact decision algorithm

5.5 Image Credits

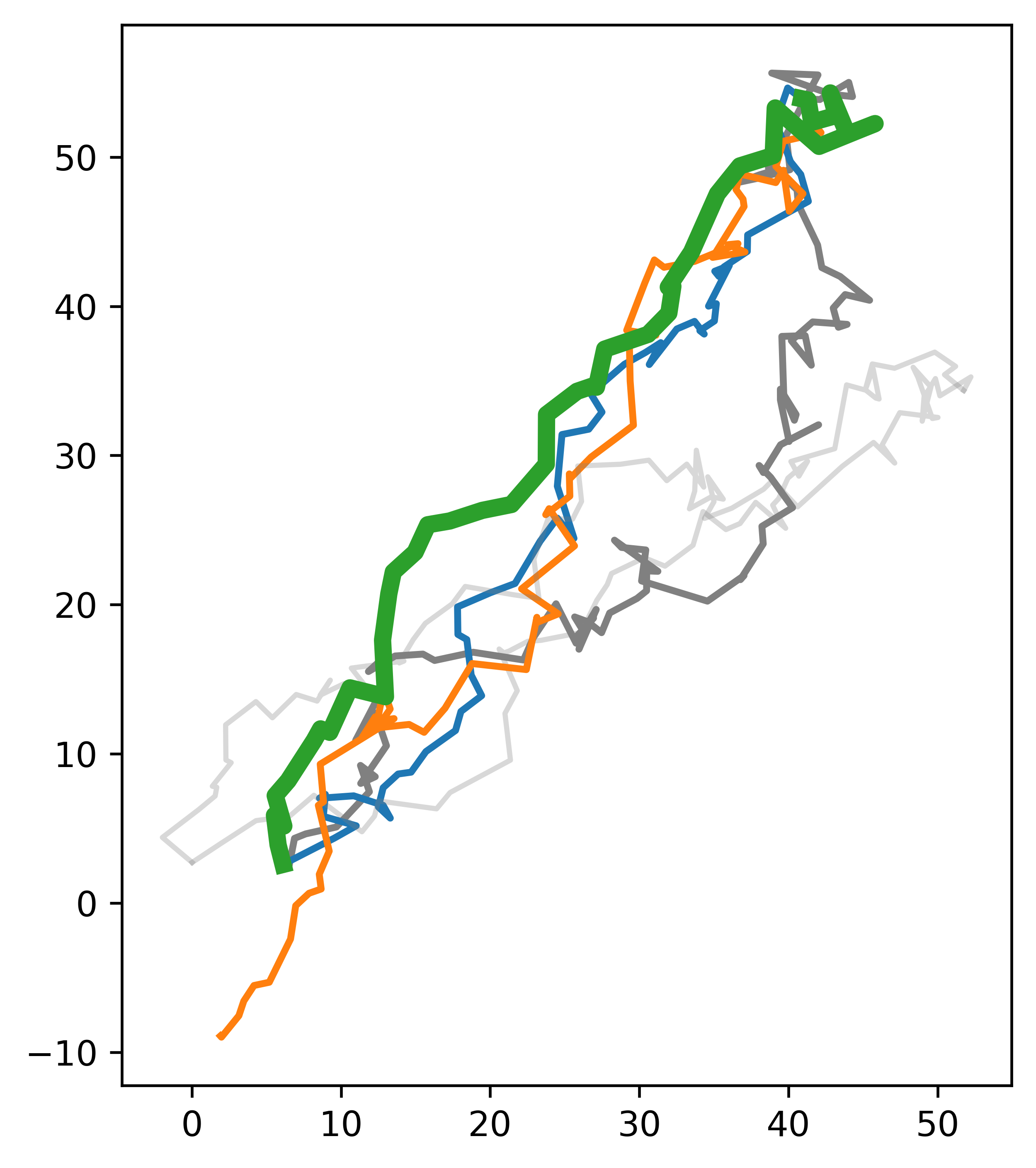
The character image is a visualization of two data points from the Character Trajectories data set.

5.6 Implementation History

An initial version using floating point arithmetic was developed by the authors while working at the Max-Planck Institute for Informatics in Saarbrücken, Germany. André Nusser, together with Sebastien Loriot and Andreas Fabri, introduced the usage of interval arithmetic and square root extensions to alleviate issues stemming from rounding errors and hence ensuring correctness of the computation.